已知⊙O₁和⊙O₂的半径分别为2和3，两圆相交于点A、B，且AB=2，则O₁O₂的长为________．

2 $\text{[math]}$ ± $\text{[math]}$
分析：利用连心线垂直平分公共弦的性质，构造直角三角形利用勾股定理及有关性质解题．
解答：

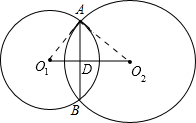
解：如图，∵⊙O₁与⊙O₂相交于A、B两点，
∴O₁O₂⊥AB，且AD=BD；
又∵AB=2，
∴AD=1，
∵⊙O₁和⊙O₂的半径分别为2和3，
∴在Rt△AO₁D中，根据勾股定理知O₁D= $\text{[math]}$ = $\text{[math]}$ ；
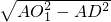
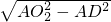
在Rt△AO₂D中，根据勾股定理知O₂D= $\text{[math]}$ =2 $\text{[math]}$ ，
∴O₁O₂=O₁D+O₂D= $\text{[math]}$ +2 $\text{[math]}$ ；
同理知，当小圆圆心在大圆内时，解得O₁O₂=2 $\text{[math]}$ - $\text{[math]}$ ．
故答案是：2 $\text{[math]}$ ± $\text{[math]}$ ．
点评：本题主要考查了圆与圆的位置关系，勾股定理等知识点．注意，解题时要分类讨论，以防漏解．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

6、已知⊙O₁和⊙O₂的半径分别为3cm和4cm，圆心距O₁O₂=6cm，那么⊙O₁和⊙O₂的位置关系是（　　）

A、内切

B、相交

C、外切

D、外离

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，已知⊙O₁和⊙O₂的半径分别为R、r，连接O₁O₂交⊙O₁于点M、交⊙O₂于点N．将一个直角三角尺的直角顶点C放在直线O₁O₂的上方，让两个直角边所在的直线分别经过点M、N，CM交⊙O₁于点A，CN交⊙O₂于点B．
（1）求证：O₁A∥O₂B；
（2）直线AB和直线O₁O₂能否平行？若能够，试指出什么条件下，AB∥O₁O₂；若不能，试说明理由．
（3）是否存在一点C，使CM•CA=CN•CB？若存在，请说明如何确定点C的位置，并证明你的结论；如果不存在，请说明理由．