

 x2-1交点坐标,横坐标x的范围就在两个交点之间.
x2-1交点坐标,横坐标x的范围就在两个交点之间.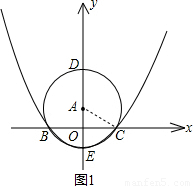
 DE=2
DE=2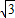
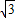 ,0),B(
,0),B(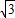 ,0)
,0)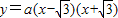 ,
,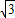 )(0+
)(0+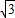 )
)
 (x-
(x-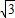 )(x+
)(x+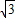 )=
)= x2-1(2分).
x2-1(2分).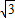
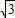 ,0),B(-
,0),B(-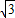 ,0)
,0)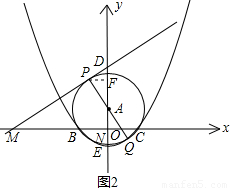
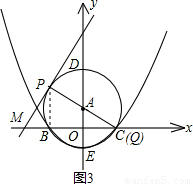
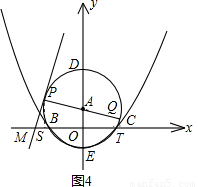
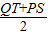
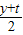
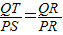
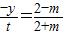 &&(1)
&&(1)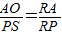
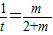 &&(2)
&&(2)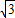
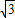 ,2)
,2)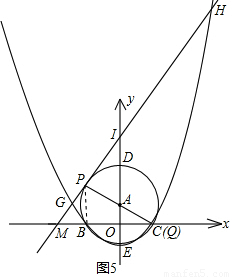 0°
0°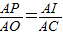
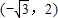 ,
,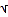 3 k+5.
3 k+5.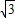 ,
,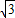 x+5(7分)
x+5(7分) x2-1交于G、H两点
x2-1交于G、H两点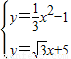
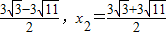
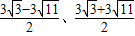
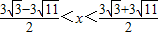 (9分)
(9分)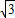 ,2)
,2)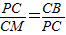
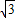 ,PC=4
,PC=4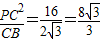
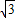 -m=
-m=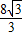
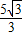 .
.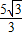 ,0).
,0).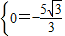 k+b2=-
k+b2=-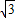 k+b.
k+b.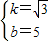
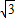 x+5(7分)
x+5(7分)

 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:2003年全国中考数学试题汇编《反比例函数》(01)(解析版) 题型:选择题
 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

查看答案和解析>>
科目:初中数学 来源:2003年北京市海淀区中考数学试卷(解析版) 题型:选择题
| 体温计的读数t(℃) | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 水银柱的长度l(mm) | 56.5 | 62.5 | 68.5 | 74.5 | 80.5 | 86.5 | 92.5 | 98.5 |

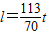


查看答案和解析>>
科目:初中数学 来源:2003年北京市海淀区中考数学试卷(解析版) 题型:选择题
 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

查看答案和解析>>
科目:初中数学 来源:2003年北京市海淀区中考数学模拟试卷(解析版) 题型:解答题
 ,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.
,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边. ,若△ABC的周长为10,求抛物线的解析式;
,若△ABC的周长为10,求抛物线的解析式; 交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com