
 ,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.
,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边. ,若△ABC的周长为10,求抛物线的解析式;
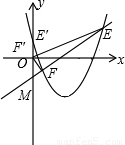
,若△ABC的周长为10,求抛物线的解析式; 交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.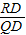 =
=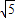 ,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.
,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.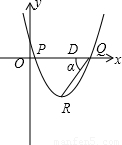 (1)证明:y=x2-(a+b)x+
(1)证明:y=x2-(a+b)x+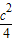
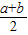 ,
,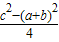 ),
),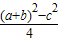
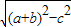 ,DQ=
,DQ=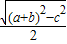 ,tanα=
,tanα=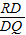 =
=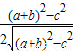 =
=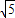
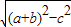 =2
=2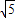 ,
,
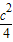
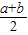 =a,
=a,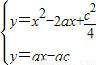
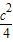 =0
=0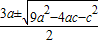
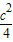 )在y轴正半轴.
)在y轴正半轴.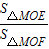 =
=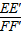 =
=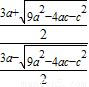 =5
=5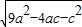 =2a
=2a

科目:初中数学 来源:2003年北京市海淀区中考数学模拟试卷(解析版) 题型:填空题
 )关于y轴对称,如果函数
)关于y轴对称,如果函数 的图象经过点A,那么k= .
的图象经过点A,那么k= .查看答案和解析>>
科目:初中数学 来源:2003年北京市海淀区中考数学模拟试卷(解析版) 题型:选择题
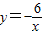 与一次函数y=mx-2的图象都经过点P(a,1),则a、m分别为( )
与一次函数y=mx-2的图象都经过点P(a,1),则a、m分别为( )



查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市青春中学中考数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2003年北京市海淀区中考数学模拟试卷(解析版) 题型:选择题
 的结果为( )
的结果为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com