练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，在四边形ACDE中，ED=CA，ED∥CA，C为AB的中点，BE与CD相交于点F，求证：EF=BF．

    分析 欲证明EF=BF，只要证明△EDF≌△BCF即可．

    解答 证明：∵DE∥AB，
    ∴∠DEF=∠B，
    ∵DA=AC，AC=BC，
    ∴DE=BC，
    在△EDF和△BCF中，
    $\left\{\begin{array}{l}{∠DEF=∠B}\\{∠EFD=∠BFC}\\{DE=CB}\end{array}\right.$，
    ∴△EDF≌△BCF，
    ∴EF=BF．

    点评 本题考查全等三角形的判定和性质、平行线的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

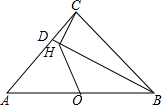    11．如图，△ABC中，∠ACB=90°，AC=BC=3，点D在AC上，CD=1，连接BD，过点C作CH⊥BD于点H，O为AB中点，连接OH，则OH的长为$\frac{3\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成（计件奖励工资=销售每件的奖励金额×销售件数），如表是甲、乙两位职工某月的工资情况．
    职工甲乙
    月销售件数（件）200180
    月工资（元）18001700
    （1）求职工的月基本保障工资和销售每件产品的奖励金额各是多少元？
    （2）若职工丙今年5月份的工资为2000元，那么丙该月销售了多少件产品？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．阅读理解题例：若x=123456789×123456786，y=123456788×123456787，试比较x、y的大小．
    解：设123456788=a，那么x=（a+1）（a-2）=a2-a-2
    y=a（a-1）=a2-a，∵x-y=（a2-a-2）-（a2-a）=-2＜0
    ∴x＜y．
    问题：计算：3.456×2.456×5.456-3.4563-1.4562．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．在平面直角坐标系中，点A（5，0），点B是y轴上一点，若AB=$\sqrt{41}$，则点B的坐标为B（0，±4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知y是x的函数，自变量x的取值范围是x＞0，下表是y与x的几组对应值．
    x…1245689…
    y…3.921.950.980.782.442.440.78…
    小风根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象和性质进行了探究．
    下面是小风的探究过程，请补充完整：
    （1）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
    （2）根据画出的函数图象，写出：
    ①x=7对应的函数值y约为3.0．
    ②该函数的一条性质：该函数没有最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）16×2-4+（-$\frac{1}{3}$）0÷（-$\frac{1}{3}$）-2
    （2）x4-（x-3）（x+3）（x2+9）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

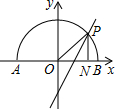    10．如图，半径为1的半圆的圆心在原点，直径AB在x轴上，过原点的任意一条半径与半圆交于点P，过P作PN垂直于x轴，N为垂足，则∠OPN的平分线过定点（　　）
    A．（0，-1）B．（0，-$\frac{4}{5}$）C．（0，-$\frac{3}{5}$）D．（0，-$\frac{6}{5}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（-1，0），B（3，0），C（0，-3）三点，直线l是抛物线的对称轴．
    （1）求抛物线的函数关系式；
    （2）点M是直线l上的动点，且△MAC为等腰三角形，请直接写出所有符合条件的点M的坐标；
    （3）将抛物线向右平移h（h＞0）个单位，所得新抛物线与x轴交于点A1、B1，与原抛物线的交点为P，连结PA1、PB1，当△PA1B1的面积为2时，求此时h的值．

    查看答案和解析>>

    同步练习册答案