
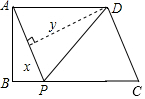
 如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=3,AD=4,BC=3$\sqrt{3}$,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=3,AD=4,BC=3$\sqrt{3}$,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )| A. | 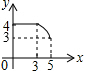 | B. | 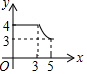 | C. | 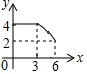 | D. | 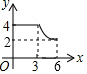 |
分析 分两种情况:(1)当点P在AB上移动时,点D到直线PA的距离不变,恒为4;(2)当点P在BC上移动时,根据相似三角形判定的方法,判断出△PAB∽△ADE,即可判断出y=$\frac{12}{x}$(3<x≤6),据此判断出y关于x的函数大致图象是哪个即可.
解答 解:根据题意,分两种情况:
(1)当点P在AB上移动时,
点D到直线PA的距离为:
y=DA=4(0≤x≤3),即点D到PA的距离为AD的长度,是定值4;
(2)当点P在BC上移动时,
∵AB=3,BC=3$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{3})^{2}}$=6,
∵AD∥BC,
∴∠APB=∠DAE,
∵∠ABP=∠AED=90°,
∴△PAB∽△ADE,
∴$\frac{PA}{AD}$=$\frac{AB}{DE}$,
∴$\frac{x}{4}$=$\frac{3}{y}$,
∴y=$\frac{12}{x}$(3<x≤6),
综上,纵观各选项,只有D选项图形符合.
故选:D.
点评 本题考查了动点问题函数图象,关键是利用了相似三角形的判定与性质,难点在于根据点P的位置分两种情况讨论.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{12}$ | C. | $\sqrt{7}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1+x}$ | B. | $\sqrt{2x+5}$ | C. | $\sqrt{3x-4}$ | D. | $\sqrt{4-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-1 | B. | a=0 | C. | a=$\frac{1}{2}$ | D. | a=$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com