
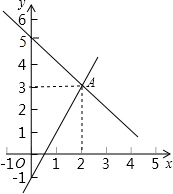
 如图,
如图,分析 (1)先利用待定系数法分别求出两直线的解析式,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案;
(2)根据函数图象与坐标轴的交点坐标和两函数的交点坐标利用三角形的面积公式进行计算即可.
解答 解:(1)设过点(0,5)和点(2,3)的解析式为y=kx+b,
则$\left\{\begin{array}{l}{b=5}\\{2k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
所以该一次函数解析式为y=-x+5;
设过点(0,-1)和点(2,3)的解析式为y=mx+n,
则$\left\{\begin{array}{l}{n=-1}\\{2m+n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$,
所以该一次函数解析式为y=2x-1,
所以点A的坐标可以看成是方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$解.
故答案为:$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$;
(2)围成的三角形的面积为:S=$\frac{1}{2}$[5-(-1)]×2=6.
点评 本题考查了一次函数与二元一次方程(组)的知识,函数图象交点坐标为两函数解析式组成的方程组的解.也考查了待定系数法求次函数解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:一次函数y=2x-4
已知:一次函数y=2x-4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
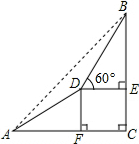 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com