
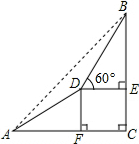
 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 在Rt△AFD中,根据AD=200米,∠DAF=30°,求出DF、AF的长度,然后四边形DFCE是矩形,设DE=x米,在Rt△BDE中,用x表示出BE的长度,然后根据AC=BC,代入求出x的值,继而可求得山高.
解答 解:在Rt△AFD中,
∵AD=200米,∠DAF=30°,
∴DF=$\frac{1}{2}$AD=$\frac{1}{2}$×200=100(米),
AF=AD•cos30°=100$\sqrt{3}$(米),
∵DF⊥AC,DE⊥BC,
∴四边形DFCE是矩形,
∴EC=DF=100米,
设DE=x米,则FC=x米,
在Rt△BDE中,
∵∠BDE=60°,
∴BE=tan60°•DE=$\sqrt{3}$x(米),
∵∠BAC=45°,∠C=90°,
∴∠ABC=45°,
∴AC=BC,
∵AC=AF+FC=(100$\sqrt{3}$+x)米,
BC=BE+EC=($\sqrt{3}$x+100)米,
解得:x=100,
∴BC=BE+EC=100$\sqrt{3}$+100≈273(米),
答:山的高度BC约为273米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识解直角三角形,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
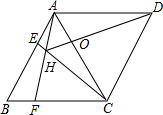 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com