
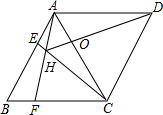
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 由菱形ABCD中,AB=AC,易证得△ABC是等边三角形,则可得∠B=∠EAC=60°,由SAS即可证得△ABF≌△CAE;则可得∠BAF=∠ACE,利用三角形外角的性质,即可求得∠AHC=120°;在HD上截取HK=AH,连接AK,易得点A,H,C,D四点共圆,则可证得△AHK是等边三角形,然后由AAS即可证得△AKD≌△AHC,则可证得AH+CH=DH.
解答 解:∵四边形ABCD是菱形,
∴AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形
∴∠B=∠EAC=60°,
在△ABF和△CAE中,
$\left\{\begin{array}{l}{BF=AE}\\{∠B=∠EAC}\\{BC=AC}\end{array}\right.$,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;
故②正确;
在HD上截取HK=AH,连接AK,
∵∠AHC+∠ADC=120°+60°=180°,
∴点A,H,C,D四点共圆,
∴∠AHD=∠ACD=60°,∠ACH=∠ADH,
∴△AHK是等边三角形,
∴AK=AH,∠AKH=60°,
∴∠AKD=∠AHC=120°,
在△AKD和△AHC中,
$\left\{\begin{array}{l}{∠AKD=∠AHC}\\{∠ADH=∠ACH}\\{AD=AC}\end{array}\right.$,
∴△AKD≌△AHC(AAS),
∴CH=DK,
∴DH=HK+DK=AH+CH;
故③正确;
故选D.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
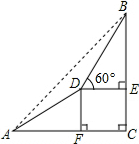 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | BE=DF | B. | AG=GH=HC | C. | EG=$\frac{1}{2}$BG | D. | S△ABE=2S△AGE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com