
分析 根据完全平方式的特点把4-2$\sqrt{3}$化成($\sqrt{3}$-1)2的形式,再代入a的值运用平方差公式计算,即可得出结果.
解答 解:∵a=$\sqrt{3}$+1,
∴(4-2$\sqrt{3}$)a2+(1-$\sqrt{3}$)a
=($\sqrt{3}$-1)2a2-($\sqrt{3}$-1)a
=[($\sqrt{3}$-1)a]2-($\sqrt{3}$-1)a
=[($\sqrt{3}$-1)($\sqrt{3}$+1]2-($\sqrt{3}$-1)($\sqrt{3}$+1)
=(3-1)2-(3-1)
=4-2
=2.
点评 本题考查了二次根式的化简求值、完全平方公式、平方差公式;熟练掌握完全平方公式和平方差公式是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
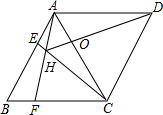 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
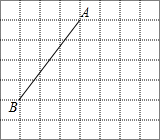 线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com