
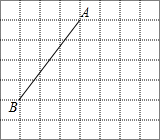
 线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.分析 (1)利用旋转的性质画图,其中弧BC为点B经过的路径;
(2)先利用网格的特点和勾股定理计算出AB=5,然后根据扇形的面积公式求解;
(3)圆锥的底面圆的半径为r,利用圆锥侧面展开图为扇形,扇形的弧长为底面圆的周长和弧长公式得到2πr=$\frac{90•π•5}{180}$,然后解关于r的方程即可.
解答 解:(1)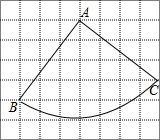 如图,弧BC为点B经过的路径;
如图,弧BC为点B经过的路径;
(2)AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以线段AB扫过的区域的面积=$\frac{90•π•{5}^{2}}{360}$=$\frac{25}{4}$π;
(3)设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{90•π•5}{180}$,
解得r=$\frac{5}{4}$,
即圆锥的底面圆半径为$\frac{5}{4}$.
故答案为$\frac{25}{4}$π,$\frac{5}{4}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了扇形面积的计算和圆锥的计算.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
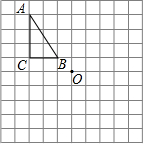 已知,如图△ABC,请在网格纸中画.
已知,如图△ABC,请在网格纸中画.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
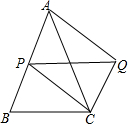 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )
如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA、PC为边作平行四边形PAQC,则对角线PQ的最小值为( )| A. | 6 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
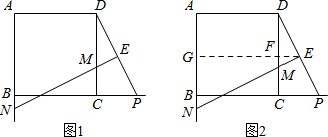
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
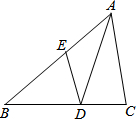 如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
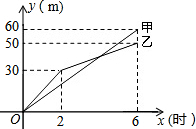 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com