
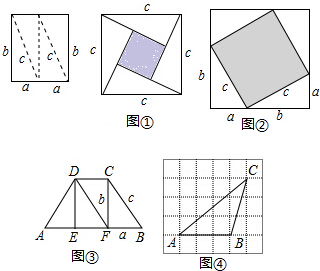
���� ��1�������ĸ�ȫ�ȵ�ֱ�������ε����+��Ӱ����С�����ε����=�������ε������������ֵ������֤����
��2���ɣ�1���н��������c��ֵ���ٸ����ܳ���ʽ���ɵó�����ABCD���ܳ���
��3���ȸ��ݸߵĶ��廭��BD���ɣ�1���н������AC�ij����ٸ��ݡ�ABC�����������ʽ�����������BD�ij���
��� ��1��֤������ͼ�ã�$\frac{1}{2}$��ab��4+c2=��a+b������a+b����
�����ã�2ab+c2=a2+b2+2ab��
��a2+b2=c2��
��2���⣺��a=3��b=4��
��c=$\sqrt{{a}^{2}+{b}^{2}}$=5��
����ABCD���ܳ�Ϊ��a+c+3a+c�T4a+2c=4��3+2��5=22��
��3���⣺��ͼ4��BD�ǡ�ABC�ĸߣ�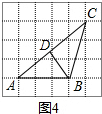
��S��ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$AB��3��AC=$\sqrt{{4}^{2}+{3}^{2}}$=5��
��BD=$\frac{3AB}{AC}$=$\frac{3��3}{5}$=$\frac{9}{5}$��
���� ���⿼���������ν����֤�����ɶ��������ɶ�����Ӧ�ã����ε��ܳ��������εĸ��������������ͬѧ�ǵ����ν�ϵ�˼�뷽����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��һ�κ���y=2x-4
��֪��һ�κ���y=2x-4�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
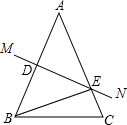 �ڡ�ABC�У�AB=AC=14cm��DΪBA���е㣬DE��AB��BC��E������EBC���ܳ�Ϊ25cm����BC��Ϊ11cm��
�ڡ�ABC�У�AB=AC=14cm��DΪBA���е㣬DE��AB��BC��E������EBC���ܳ�Ϊ25cm����BC��Ϊ11cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
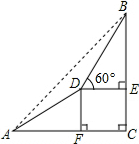 ijУ��ѧ��ȤС��Ϊ����ɽ�ߣ���ɽ��A�����ɽ��B������Ϊ45�㣬�����½�Ϊ30���ɽ��ǰ��200����D������D�����ɽ��B������Ϊ60�㣬��ͼ��ʾ����ɽ�ĸ߶�BC���������ȷ��1�ף��ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732��
ijУ��ѧ��ȤС��Ϊ����ɽ�ߣ���ɽ��A�����ɽ��B������Ϊ45�㣬�����½�Ϊ30���ɽ��ǰ��200����D������D�����ɽ��B������Ϊ60�㣬��ͼ��ʾ����ɽ�ĸ߶�BC���������ȷ��1�ף��ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
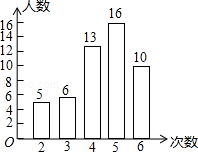 ���п�չ�ˡ�Ѱ�����㼣���Ļ��ij��ѧΪ���˽���꼶800��ѧ���ڡ�ѧ���¡��������µ��������������˰��꼶50��ѧ����һ�����������µĴ����������������ݻ��Ƴ�ͳ��ͼ�����Ƹ�У���꼶800��ѧ���ڡ�ѧ���¡��������²�����5�ε������У�������
���п�չ�ˡ�Ѱ�����㼣���Ļ��ij��ѧΪ���˽���꼶800��ѧ���ڡ�ѧ���¡��������µ��������������˰��꼶50��ѧ����һ�����������µĴ����������������ݻ��Ƴ�ͳ��ͼ�����Ƹ�У���꼶800��ѧ���ڡ�ѧ���¡��������²�����5�ε������У�������| A�� | 384 | B�� | 256 | C�� | 160 | D�� | 416 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com