
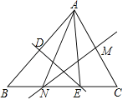
【题目】如图,△ABC中,∠BAC=80°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,NE=6,则∠NAE=______°,△EAN的周长=_____.
【答案】40° 24
【解析】
(1)根据三角形内角和定理可求∠B+∠C,根据垂直平分线性质,EA=EB,NA=NC,则∠EAB=∠B,∠NAC=∠C,从而可得∠BAC=∠BAE+∠NAC-∠EAN=∠B+∠C-∠EAN,即可得到∠EAN=∠B+∠C-∠BAC,即可得解.
(2)根据线段的垂直平分线得出BE=AE,AN=CN,从而可△AEN的周长=2BC;
(1)∵∠BAC=70°,
∴∠B+∠C=180°-70°=110°,
∵AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,
∴EA=EB,NA=NC,
∴∠EAB=∠B,∠NAC=∠C,
∴∠BAC=∠BAE+∠NAC-∠EAN=∠B+∠C-∠EAN,
∴∠EAN=∠B+∠C-∠BAC,
=110°-70°
=40°.
(2)∵点E、N分别是AB、AC边的垂直平分线与BC的交点,
∴BE=AE,AN=CN.
∴△AEN的周长=AE+AN+EN=BE+NC+EN=BC+2NE=12+12=24;
故答案为24


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
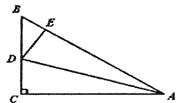
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④若AC=4BE,则S△ABC=8S△BDE其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
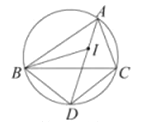
【题目】如图,I是ABC的内心,AI向延长线和△ABC的外接圆相交于点D,连接BI,BD,DC下列说法中错误的一项是( )
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI熏合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
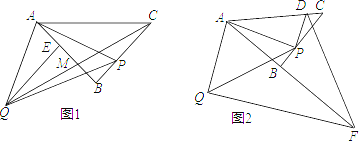
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
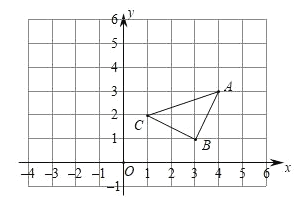
【题目】如图,若△A1B1C1是由△ABC平移后得到的,且△ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣5,y+2).
(1)在下图方格中画出△A1B1C1.
(2)求点A1、B1、C1的坐标.
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,试探究并回答下列问题:
,试探究并回答下列问题:
(1)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?并说明理由;
?并说明理由;
(2)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?如果存在,那么它的位置是唯一的吗?
?如果存在,那么它的位置是唯一的吗?
(3)当点![]() 到
到![]() 两点的距离之和等于
两点的距离之和等于![]() 时,试说明点
时,试说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
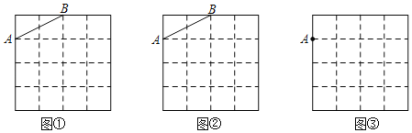
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两名同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
①填空:此次试验中“5点朝上”的频率为________;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图法加以说明,并求出其概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
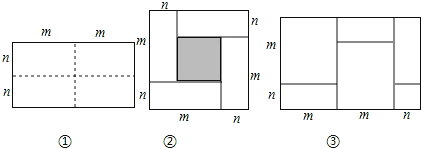
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com