
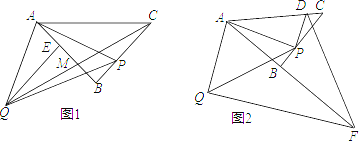
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
【答案】(1)证明见详解;(2)2;(3)式子值不变,理由见详解.
【解析】
(1)根据题目中的信息可以得到AQ=AP,∠QEA与∠ABP之间的关系,∠QAE与∠APB之间的关系,从而可以解答本题;
(2)由第一问中的两个三角形全等,可以得到各边之间的关系,然后根据题目中的信息找到PC与MB的关系,从而可以解答本题;
(3)作合适的辅助线,构造直角三角形,通过三角形的全等可以找到所求问题需要的边之间的关系,从而可以解答本题.
(1)证明:∵△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.
∴AP=AQ,∠ABQ=∠QEA=90°,∠QAE+∠BAP=∠BAP+∠APB=90°,
∴∠QAE=∠APB,
在△PAB和△AQE中,
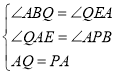
∴△PAB≌△AQE(AAS);
(2) ∵△PAB≌△AQE,
∴AE=PB,
∵AB=CB,
∴QE=CB.
在△QEM和△CBM中,
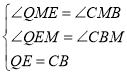
∴△QEM≌△CBM(AAS),
∴ME=MB,
∵AB=CB,AE=PB,PC=2PB,
∴BE=PC,
∵PC=2PB,
∴PC=2MB,
∴![]()
(3)式子![]() 的值不会变化.
的值不会变化.
如下图所示:作HA⊥AC交QF于点H,

∵QA⊥AP,HA⊥AC,AP⊥PD,
∴∠QAH+∠HAP=∠HAP+∠PAD=90°,∠AQH=∠APD=90°,
∴∠QAH=∠PAD,
∵△PAQ为等腰直角三角形,
∴AQ=AP,
在△AQH和△APD中,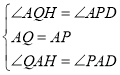
∴△AQH≌△APD(ASA),
∴AH=AD,QH=PD,
∵HA⊥AC,∠BAC=45°,
∴∠HAF=∠DAF,
在△AHF和△ADF中,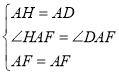
∴△AHF≌△ADF(SAS),
∴HF=DF,
∴![]()


科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.

(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
(3)如图3,若BE、DE分别六等分∠ABC、∠ADC的邻补角(即∠CBE=![]() ∠CBM,∠CDE=
∠CBM,∠CDE=![]() ∠CDN),则∠E= .
∠CDN),则∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张长方形纸片宽AB=DC=8 cm,长BC=AD=10 cm,∠B=∠C=∠D=∠BAD=90°.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.
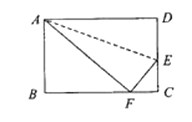
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为非负实数,关于x的方程x2﹣(k+1)x+k=0和kx2﹣(k+2)x+k=0.
(1)试证:前一个方程必有两个非负实数根;
(2)当k取何值时,上述两个方程有一个相同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOD=150°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当射线OB绕点O在∠AOD内旋转时,
∠MON= °;
(2)OC也是∠AOD内的射线,如图2,若∠BOC=m°,OM平分∠AOC,ON平分∠BOD,
求∠MON的大小(用含m的式子表示);
(3)在(2)的条件下,若m=20,∠AOB=10°,当∠BOC在∠AOD内部绕O点以每秒2°的速度逆时针旋转t秒,如图3,若3∠AOM=2∠DON时,求t的值.
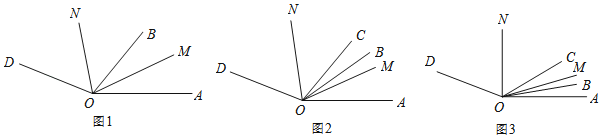
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=80°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,NE=6,则∠NAE=______°,△EAN的周长=_____.
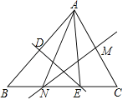
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com