
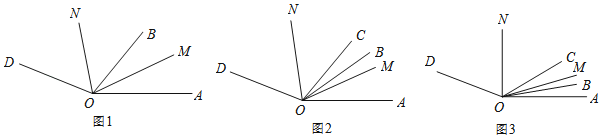
【题目】已知:∠AOD=150°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当射线OB绕点O在∠AOD内旋转时,
∠MON= °;
(2)OC也是∠AOD内的射线,如图2,若∠BOC=m°,OM平分∠AOC,ON平分∠BOD,
求∠MON的大小(用含m的式子表示);
(3)在(2)的条件下,若m=20,∠AOB=10°,当∠BOC在∠AOD内部绕O点以每秒2°的速度逆时针旋转t秒,如图3,若3∠AOM=2∠DON时,求t的值.
【答案】(1)75;(2)(75-![]() m)°;(3)t为19秒.
m)°;(3)t为19秒.
【解析】
(1)根据角平分线的定义,以及角度和的关系,可得∠MON=![]() ∠AOD即可得出;
∠AOD即可得出;
(2)根据角平分线的定义,得出∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,利用角度和与差的关系,得出∠MON=∠MOC+∠BON﹣∠BOC,角度代换即可得出结果;
∠BOD,利用角度和与差的关系,得出∠MON=∠MOC+∠BON﹣∠BOC,角度代换即可得出结果;
(3)由题意知,∠AOM=![]() (10+2t+20°),∠DON=
(10+2t+20°),∠DON=![]() (150﹣10﹣2t)°,根据3∠AOM=2∠DON,列出方程求解即可.
(150﹣10﹣2t)°,根据3∠AOM=2∠DON,列出方程求解即可.
解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠MOB=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠MOB+∠BON,
=![]() ∠AOB+
∠AOB+![]() ∠BOD,
∠BOD,
=![]() ∠AOD,
∠AOD,
=![]() ×150°,
×150°,
=75°,
故答案为:75;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∠MON=∠MOC+∠BON﹣∠BOC
=![]() ∠AOC+
∠AOC+![]() ∠BOD﹣∠BOC
∠BOD﹣∠BOC
=![]() (∠AOC+∠BOD)﹣∠BOC
(∠AOC+∠BOD)﹣∠BOC
=![]() (∠AOB+∠BOC+∠BOD)﹣∠BOC
(∠AOB+∠BOC+∠BOD)﹣∠BOC
=![]() (∠AOD+∠BOC)﹣∠BOC
(∠AOD+∠BOC)﹣∠BOC
=![]() ×(150°+m°)﹣m°
×(150°+m°)﹣m°
=(75-![]() m)°,
m)°,
故答案为:(75-![]() m)°;
m)°;
(3)∵∠AOM=![]() ∠AOC=
∠AOC=![]() (10+2t+20°)=(15+t)°,
(10+2t+20°)=(15+t)°,
∠DON=![]() ∠BOD=
∠BOD=![]() (150﹣10﹣2t)°=(70-t)°,
(150﹣10﹣2t)°=(70-t)°,
又∵3∠AOM=2∠DON,
∴3(15+t)=2(70﹣t),
得t=19.
答:t为19秒,
故答案为:19秒.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
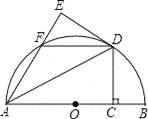
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
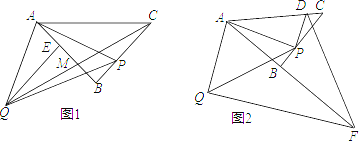
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,试探究并回答下列问题:
,试探究并回答下列问题:
(1)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?并说明理由;
?并说明理由;
(2)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?如果存在,那么它的位置是唯一的吗?
?如果存在,那么它的位置是唯一的吗?
(3)当点![]() 到
到![]() 两点的距离之和等于
两点的距离之和等于![]() 时,试说明点
时,试说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
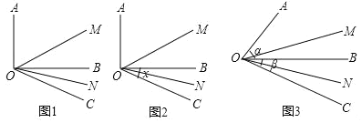
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com