
【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
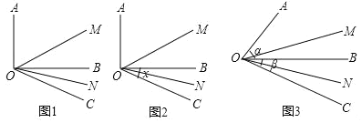
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
【答案】(1)45°;(2)能,![]() ;(3)能,
;(3)能,![]() ;(4)
;(4)![]()
【解析】
(1)根据题意可知,∠AOC=120°,由OM平分∠AOC,ON平分∠BOC;推出∠MOC=∠AOC=60°,∠CON= ![]() ∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即可求出∠MON=45°;
∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即可求出∠MON=45°;
(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;
(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得解.
(4)由(1)、(2)、(3)的结果中,∠MON的度数与∠BCO无关,∠MON= ![]() .
.
(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=60°,∠CON= ![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOC-∠CON=60°-15°=45°;
(2)能.
∵∠AOB=90°,∠BOC=x,
∴∠AOC=90°+x,
∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (90°+x°)=45°+
(90°+x°)=45°+ ![]() x,
x,
∴∠CON= ![]() ∠BOC=
∠BOC= ![]() x,
x,
∴∠MON=∠MOC-∠CON=45°+ ![]() x-
x- ![]() x=45°.
x=45°.
(3)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC= ![]() ∠BOC=
∠BOC= ![]() ,
,
∴∠MON=∠MOC-∠NOC= ![]() (α+β)-
(α+β)-![]() =
=![]() .
.
(4)规律:∠MON的度数与∠BCO无关,∠MON=![]() .理由如下:
.理由如下:
∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (α+β)-
(α+β)-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
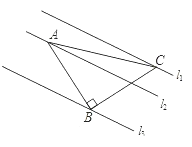
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1、l2之间的距离为2,l2、l3之间的距离为3,则AC的长是_________;
查看答案和解析>>
科目:初中数学 来源: 题型:
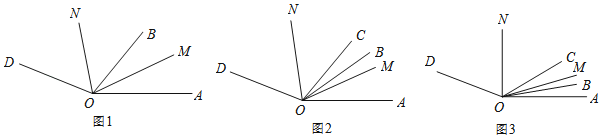
【题目】已知:∠AOD=150°,OB,OM,ON是∠AOD内的射线.
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当射线OB绕点O在∠AOD内旋转时,
∠MON= °;
(2)OC也是∠AOD内的射线,如图2,若∠BOC=m°,OM平分∠AOC,ON平分∠BOD,
求∠MON的大小(用含m的式子表示);
(3)在(2)的条件下,若m=20,∠AOB=10°,当∠BOC在∠AOD内部绕O点以每秒2°的速度逆时针旋转t秒,如图3,若3∠AOM=2∠DON时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答提出的问题.
我们知道:一个数![]() 的绝对值可以表示成
的绝对值可以表示成![]() ,它是一个非负数,在数轴上,
,它是一个非负数,在数轴上,![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说
这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说![]() 表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说
表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离,它也是2,所以说
这个数在数轴上所对应的点到原点的距离,它也是2,所以说![]() ,严格来说,在数轴上,一个数
,严格来说,在数轴上,一个数![]() 在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为
在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为![]() ,但平时我们都写成
,但平时我们都写成![]() ,原因你明白.
,原因你明白.
(1)若给定![]() ,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的
,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的![]() ;
;
(2)实际上,对于数轴上任意两个数![]() 之间的距离我们也可以表示为
之间的距离我们也可以表示为![]() ,反过来,
,反过来,![]() 这个绝对值的几何意义就是:数轴上表示
这个绝对值的几何意义就是:数轴上表示![]() 与
与![]() 这两个数的点之间的距离,你能结合上面的叙述,解释
这两个数的点之间的距离,你能结合上面的叙述,解释![]() 的几何意义吗?请按你的理解说明:
的几何意义吗?请按你的理解说明:![]() 呢,如果能解释这个,你了不起;
呢,如果能解释这个,你了不起;
(3)若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
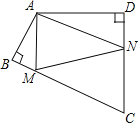
A. 130°B. 120°C. 110°D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1),
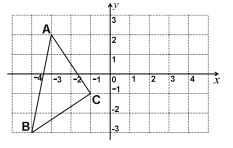
(1)请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各点坐标;
(2)在y轴上找一点P,使△APC的周长最短。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
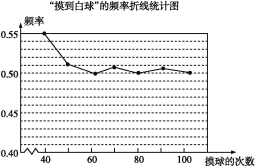
(1)请估计:当n足够大时,摸到白球的频率将会稳定在 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com