
【题目】如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1),
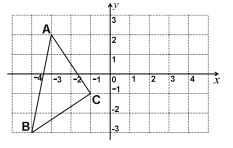
(1)请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各点坐标;
(2)在y轴上找一点P,使△APC的周长最短。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
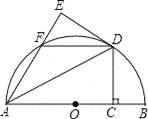
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,试探究并回答下列问题:
,试探究并回答下列问题:
(1)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?并说明理由;
?并说明理由;
(2)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?如果存在,那么它的位置是唯一的吗?
?如果存在,那么它的位置是唯一的吗?
(3)当点![]() 到
到![]() 两点的距离之和等于
两点的距离之和等于![]() 时,试说明点
时,试说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
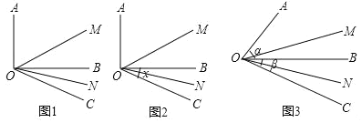
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两名同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
①填空:此次试验中“5点朝上”的频率为________;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图法加以说明,并求出其概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 | 优惠办法 |
少于200元 | 不予优惠 |
低于500元但不低于200元 | 九折优惠 |
500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(1)王老师一次性购物600元,他实际付款 元.
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款 元,当x大于或等于500元时,他实际付款 元.(用含x的代数式表示).
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的代数式表示:两次购物王老师实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是一个数值转换机的示意图.
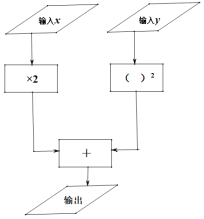
(1)当输入x=-4,y=1时,则输出结果为 ,当输入x=-1,y=2,则输出结果为 .
(2)用含x、y的代数式表示输出结果为 .
(3)若输入x的值为1,输出结果为11时,求输入y的值.
(4)若(1)中输出的两个结果依次对应数轴上的点A,B,点C为A、B之间的一个动点,若将数轴以点C为折点,将此数轴向右对折,若A点与数轴上的D点重合,且B、D两点之间的距离为1,则点C在数轴上表示的数为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。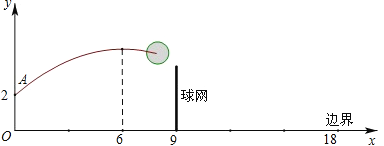
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com