
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。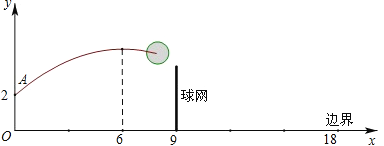
【答案】(1)y=![]() (x-6)2+2.6
(x-6)2+2.6
(2)球能越过网;球会过界
(3)h≥![]()
【解析】
试题(1)利用h=2.6将点(0,2),代入解析式求出即可;
(2)利用当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45,当y=0时,
(x﹣6)2+2.6=2.45,当y=0时,![]() ,分别得出即可;
,分别得出即可;
(3)根据当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),以及当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2)时分别得出h的取值范围,即可得出答案.
试题解析:解:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣![]() ,
,
故y与x的关系式为:y=﹣![]() (x﹣6)2+2.6,
(x﹣6)2+2.6,
(2)当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45>2.43,
(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,![]() ,
,
解得:x1=6+2![]() >18,x2=6﹣2
>18,x2=6﹣2![]() (舍去)
(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
![]() ,
,
解得: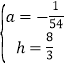 ,
,
此时二次函数解析式为:y=﹣![]() (x﹣6)2+
(x﹣6)2+![]() ,
,
此时球若不出边界h≥![]() ,
,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
![]() ,
,
解得: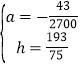 ,
,
此时球要过网h≥![]() ,
,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1),
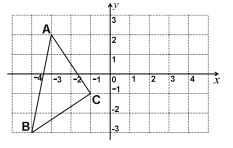
(1)请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各点坐标;
(2)在y轴上找一点P,使△APC的周长最短。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
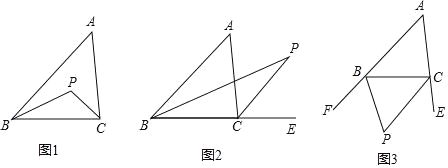
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+![]() ∠A.
∠A.
(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
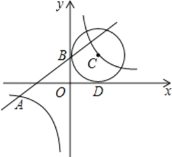
【题目】(题文)如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当![]() <
<![]() <0时,写出x的取值范围.
<0时,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北向东驶去,若自行车与摩托车每秒分别行驶![]() 米、
米、![]() 米,则
米,则![]() 秒后两车相距( )米.
秒后两车相距( )米.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
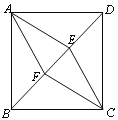
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,分别在OM、ON上截取OA=OB=3 cm,过B作BC⊥OM于C,再过B作射线BD⊥BC于B,连结AB.
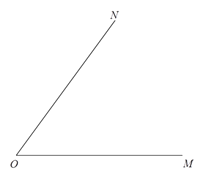
(1)画出图形;
(2)观察图形,写出直观估计∠ABC与∠MON的关系式;
(3)求∠NBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
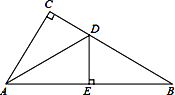
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com