
【题目】探究:
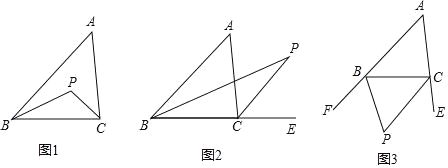
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+![]() ∠A.
∠A.
(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
【答案】(1)见解析;(2)![]() ∠A=∠P,理由见解析;(3)∠P=90°﹣
∠A=∠P,理由见解析;(3)∠P=90°﹣![]() ∠A,理由见解析
∠A,理由见解析
【解析】
(1)根据三角形内角和定理以及角平分线的性质进行解答即可:
(2)根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果,
(3)根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.
证明:(1)∵△ABC中,∠ABC+∠ACB=180°﹣∠A.
又∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=![]() ∠ABC,
∠ABC,
∠PCB=![]() ∠ACB,
∠ACB,
∴∠PBC+∠PCB=![]() (180°﹣∠A),
(180°﹣∠A),
根据三角形内角和定理可知∠BPC=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A;
∠A;
(2)![]() ∠A=∠P,理由如下:
∠A=∠P,理由如下:
∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠PBC=![]() ∠ABC,∠PCE=
∠ABC,∠PCE=![]() ∠ACE.
∠ACE.
∵∠ACE是△ABC的外角,∠PCE是△BPC的外角,
∴∠ACE=∠ABC+∠A,∠PCE=∠PBC+∠P,
∴![]() ∠ACP=
∠ACP=![]() ∠ABC+
∠ABC+![]() ∠A,
∠A,
∴![]() ∠ABC+
∠ABC+![]() ∠A=∠PBC+∠P,
∠A=∠PBC+∠P,
∴![]() ∠A=∠P.
∠A=∠P.
(3)∠P=90°﹣![]() ∠A,理由如下:
∠A,理由如下:
∵P点是外角∠CBF和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°
∴∠P=180°﹣(∠PBC+∠PCB)
=180°﹣![]() (∠FBC+∠ECB)
(∠FBC+∠ECB)
=180°﹣![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°﹣![]() (∠A+180°)
(∠A+180°)
=90°﹣![]() ∠A.
∠A.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,试探究并回答下列问题:
,试探究并回答下列问题:
(1)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?并说明理由;
?并说明理由;
(2)是否存在一点![]() ,使它到
,使它到![]() 两点的距离之和等于
两点的距离之和等于![]() ?如果存在,那么它的位置是唯一的吗?
?如果存在,那么它的位置是唯一的吗?
(3)当点![]() 到
到![]() 两点的距离之和等于
两点的距离之和等于![]() 时,试说明点
时,试说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是一个数值转换机的示意图.
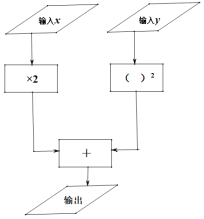
(1)当输入x=-4,y=1时,则输出结果为 ,当输入x=-1,y=2,则输出结果为 .
(2)用含x、y的代数式表示输出结果为 .
(3)若输入x的值为1,输出结果为11时,求输入y的值.
(4)若(1)中输出的两个结果依次对应数轴上的点A,B,点C为A、B之间的一个动点,若将数轴以点C为折点,将此数轴向右对折,若A点与数轴上的D点重合,且B、D两点之间的距离为1,则点C在数轴上表示的数为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
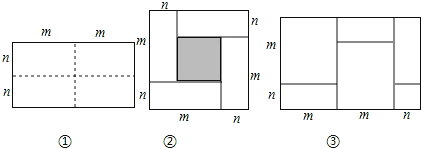
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
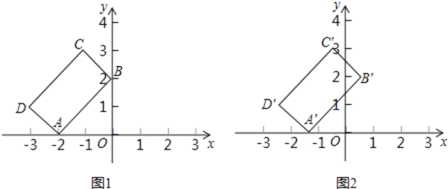
A. 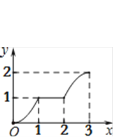 B.
B. 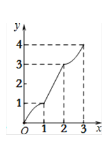 C.
C. 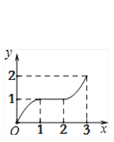 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).将△OAB进行n次变换得到△OAnBn,则An(___,__),Bn(_____,_____).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。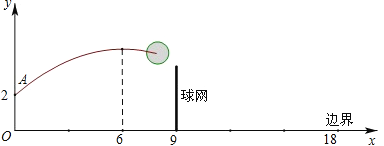
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校 5 千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程 s(千米)与时间 t(分钟)的关系,请根据图象提供的信息回答问题:
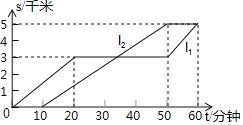
(1) 先出发,先出发了 分钟;
(2)当 t= 分钟时,小凡与小光在去图书馆的路上相遇;
(3)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括停留的时间)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com