
【题目】小凡与小光从学校出发到距学校 5 千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程 s(千米)与时间 t(分钟)的关系,请根据图象提供的信息回答问题:
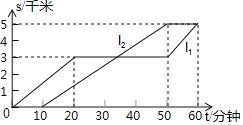
(1) 先出发,先出发了 分钟;
(2)当 t= 分钟时,小凡与小光在去图书馆的路上相遇;
(3)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括停留的时间)
科目:初中数学 来源: 题型:
【题目】探究:
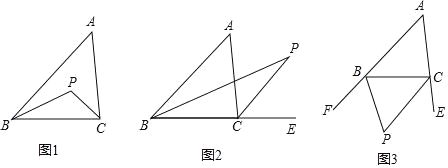
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+![]() ∠A.
∠A.
(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
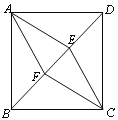
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,分别在OM、ON上截取OA=OB=3 cm,过B作BC⊥OM于C,再过B作射线BD⊥BC于B,连结AB.
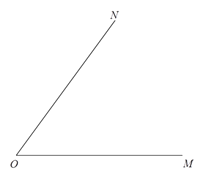
(1)画出图形;
(2)观察图形,写出直观估计∠ABC与∠MON的关系式;
(3)求∠NBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
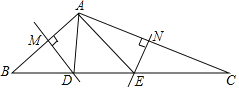
(1)若BC=8,则△ADE周长是多少?
(2)若∠BAC=118°,则∠DAE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(![]() ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
(1)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角,在图(
角,在图(![]() )中作出旋转后的
)中作出旋转后的![]() (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明).
(2)在图(![]() )中,你发现线段
)中,你发现线段![]() ,
,![]() 的数量关系是 ,直线
的数量关系是 ,直线![]() ,
,![]() 相交成 度角.
相交成 度角.
(3)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转一个锐角,得到图(
顺时针旋转一个锐角,得到图(![]() ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若![]() 绕点
绕点![]() 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如果![]() ,
,![]() 且
且![]() ,求
,求![]() 的值.
的值.
(2)数轴上表示3和5的两点距离是 .表示 -3和一5两点的距离是 .表示 3和-5两点的距离是 .
(3)在数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 的距离是 ;(用含
的距离是 ;(用含![]() 的代数式表示)如果
的代数式表示)如果![]() ,那么
,那么![]() .
.
(4)猜想对于有理数![]() ,
,![]() 能够取得的最小值是 .
能够取得的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
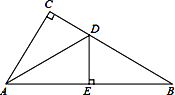
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“幸运数”;如果一个正整数
为“幸运数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“幸运数”,且
为“幸运数”,且![]() 的三十三分之一是完全平方数,则符合条件的最大一个
的三十三分之一是完全平方数,则符合条件的最大一个![]() 的值为_______.
的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com