
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
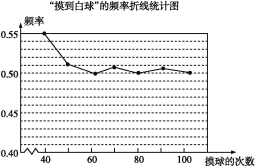
(1)请估计:当n足够大时,摸到白球的频率将会稳定在 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
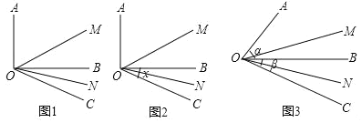
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 | 优惠办法 |
少于200元 | 不予优惠 |
低于500元但不低于200元 | 九折优惠 |
500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(1)王老师一次性购物600元,他实际付款 元.
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款 元,当x大于或等于500元时,他实际付款 元.(用含x的代数式表示).
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的代数式表示:两次购物王老师实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是一个数值转换机的示意图.
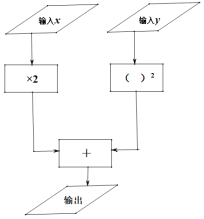
(1)当输入x=-4,y=1时,则输出结果为 ,当输入x=-1,y=2,则输出结果为 .
(2)用含x、y的代数式表示输出结果为 .
(3)若输入x的值为1,输出结果为11时,求输入y的值.
(4)若(1)中输出的两个结果依次对应数轴上的点A,B,点C为A、B之间的一个动点,若将数轴以点C为折点,将此数轴向右对折,若A点与数轴上的D点重合,且B、D两点之间的距离为1,则点C在数轴上表示的数为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于![]() ,问至少需取走多少个黄球?
,问至少需取走多少个黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
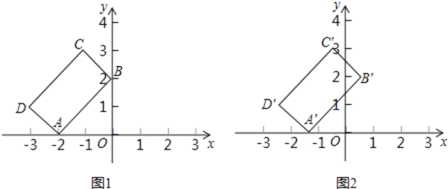
A. 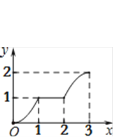 B.
B. 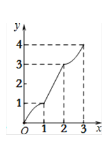 C.
C. 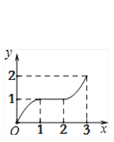 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com