
【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于![]() ,问至少需取走多少个黄球?
,问至少需取走多少个黄球?
科目:初中数学 来源: 题型:
【题目】对于正数 ![]() ,用符号
,用符号 ![]() 表示
表示 ![]() 的整数部分,例如:
的整数部分,例如: ![]() ,
, ![]() ,
, ![]() .点
.点 ![]() 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于 ![]() 轴的边长为
轴的边长为 ![]() ,垂直于
,垂直于 ![]() 轴的边长为
轴的边长为 ![]() ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点 ![]() 的矩形域是一个以
的矩形域是一个以 ![]() 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.

图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是;
(2)点 ![]() 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求 ![]() 的值;
的值;
(3)已知点 ![]() 在直线
在直线 ![]() 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积 ![]() 满足
满足 ![]() ,那么
,那么 ![]() 的取值范围是 . (直接写出结果)
的取值范围是 . (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用勾股定理可以在数轴上画出表示 ![]() 的点,请依据以下思路完成画图,并保留画图痕迹:
的点,请依据以下思路完成画图,并保留画图痕迹:![]()
(1)第一步:(计算)尝试满足 ![]() ,使其中a , b都为正整数.你取的正整数a= , b=;
,使其中a , b都为正整数.你取的正整数a= , b=;
(2)第二步:(画长为 ![]() 的线段)以第一步中你所取的正整数a , b为两条直角边长画Rt△OEF , 使O为原点,点E落在数轴的正半轴上,
的线段)以第一步中你所取的正整数a , b为两条直角边长画Rt△OEF , 使O为原点,点E落在数轴的正半轴上, ![]() ,则斜边OF的长即为
,则斜边OF的长即为 ![]() .请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
.请在下面的数轴上画图:(第二步不要求尺规作图,不要求写画法)
(3)第三步:(画表示 ![]() 的点)在下面的数轴上画出表示
的点)在下面的数轴上画出表示 ![]() 的点M , 并描述第三步的画图步骤:
的点M , 并描述第三步的画图步骤:
查看答案和解析>>
科目:初中数学 来源: 题型:
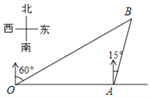
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
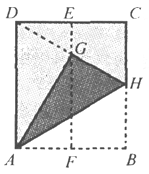
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,B , C两点的坐标分别为 ![]() ,
, ![]() ,CD⊥y轴于点D , 直线l 经过点D.
,CD⊥y轴于点D , 直线l 经过点D.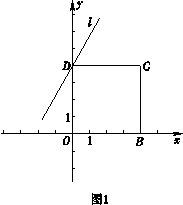
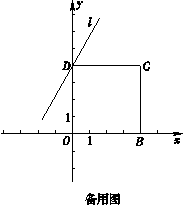
(1)直接写出点D的坐标;
(2)作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.
①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ![]() ,从而证明结论.
,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程 ![]()
![]() 满足
满足 ![]() ,那么我们称这个方程为“阿凡达”方程,已知
,那么我们称这个方程为“阿凡达”方程,已知 ![]() 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com