
【题目】已知k为非负实数,关于x的方程x2﹣(k+1)x+k=0和kx2﹣(k+2)x+k=0.
(1)试证:前一个方程必有两个非负实数根;
(2)当k取何值时,上述两个方程有一个相同的实数根.
【答案】(1)证明见解析;(2)当k=2或0或![]() 时,述两个方程有一个相同的实数根.
时,述两个方程有一个相同的实数根.
【解析】
(1)先根据根的判别式求解,再根据根与系数的关系求解即可;(2)先求出第一个方程的两个根,再分类求出即可.
(1)证明:x2﹣(k+1)x+k=0,
△=[﹣(k+1)]2﹣4k=k2﹣2k+1=(k﹣1)2≥0,
即方程关于x的方程x2﹣(k+1)x+k=0一定有两个实数根;
设方程的两根为x1,x2,
则根据根与系数的关系得:x1+x2=k+1,x1x2=k,
∵k为非负实数,
∴x1+x2=k+1>0,x1x2=k≥0,
∵由x1x2=k≥0得出方程有同号两个根或有一个根为0;
∴由x1+x2=k+1>0,x1x2=k≥0得出方程有两个正实数根或有一个根为0,
所以方程x2﹣(k+1)x+k=0必有两个非负实数根;
(2)x2﹣(k+1)x+k=0,
△=[﹣(k+1)]2﹣4k=k2﹣2k+1=(k﹣1)2≥0,
方程的根为![]() ,
,
即方程的根为k和1;
当相同的根是k时,把x=k代入方程kx2﹣(k+2)x+k=0得:k3﹣(k+2)k+k=0,
解得:k=0或k=![]() 或k=
或k=![]() ,
,
∵k为非负实数,
∴k=![]() 舍去;
舍去;
当相同的根是1时,把x=1代入方程kx2﹣(k+2)x+k=0得:k﹣(k+2)+k=0,
解得:k=2;
所以当k=2或0或![]() 时,上述两个方程有一个相同的实数根.
时,上述两个方程有一个相同的实数根.


科目:初中数学 来源: 题型:
【题目】每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.
(1)求该商场两次共购进多少瓶葡萄酒.
(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴ ∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.
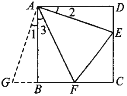
∵ ∠EAF=45°∴ ∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵ ∠1=∠2,∠1+∠3=45°.
即∠GAF=∠________.
又AG=AE,AF=AE
∴ △GAF≌△________.
∴ _________=EF,故DE+BF=EF.
(2)方法迁移:
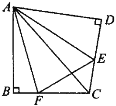
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
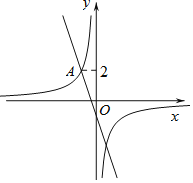
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表:

(1)求a,b的值.
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,求九年级学生可捐助的贫困生中、小学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民1月份用水8m,则应缴费2×6+3×(8-6)+5=23(元)
(1)若用户4月份共用水9.5m3,则需缴费 元;
(2)若该户居民某月缴费54元,则该户居民该月用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题1:设a、b是方程x2+x-2012=0的两个实数根,则a2+2a+b的值为________;
问题2:方程x2-2x-1=0的两个实数根分别为x1,x2,则(x1―1)(x2―1)=_______;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com