练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某山区有23名中、小学生因贫困失学需要捐助，资助一名中学生的学习费用需要a元，一名小学生的学习费用需要b元，某校学生积极捐款，我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表：

    （1）求a,b的值.

    （2）九年级学生的捐款解决了其余贫困中小学生的学习费用，求九年级学生可捐助的贫困生中、小学生人数.

    【答案】（1）a、b的值分别为800，600；（2）捐助中学生4人，小学生7人.

    【解析】

    （1）根据表格可以看出：资助2名中学生的费用+资助4名小学生的费用=4000元；资助3名中学生的费用+资助3名小学生的费用=4200元，由此可列出方程组，解方程组可得到a、b的值；
    （2）设初三年级学生可捐助的贫困中、小学生人数分别为x、y人，根据（1）中解的得数可列出二元一次方程800x+600y=7400，求其整数解即可．

    解：（1）根据题意，得

    ，

    解得：.

    答：a、b的值分别为800，600．

    （2）设初三年级学生可捐助的贫困中、小学生人数分别为x、y人，由题意得：
    800x+600y=7400，
    化简得：4x+3y=37，
    ∵x、y为正整数，x+y=23-（2+4+3+3）=11，
    联立方程组

    解得

    故答案为：捐助中学生4人，小学生7人.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列现象中，与“把弯曲的公路改直，就能缩短路程”原理一致的是（ ）

    A.从地到地架设电线，总是尽可能沿着线段架设

    B.植树时，只要定出两棵树的位置，就能确定所植树木是否成行

    C.用两个钉子就可以把木条固定在墙上

    D.体育老师画直线跑道时，常把一根长线的两端系在标枪上，插到欲画跑道两端并拉紧，得到一条参照线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

    （1）试判断直线BC与⊙O的位置关系，并说明理由；

    （2）若BD=2，BF=2，求阴影部分的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.我们规定，有理数的整数部分就是取其最接近的两个整数中的最小整数，小数部分就是用原数减去整数部分，比如，小数3.25，最接近的两个整数就是3和4，则整数部分取3，小数部分就是3.25-3=0.25，

    （1）3.14的整数部分是 ，小数部分是 ；

    （2）-3.6的整数部分是 ，小数部分是 ；

    （3）如果一个数的整数部分比小数部分大88.11，且整数部分的值恰好是小数部分的100倍，求这个数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知k为非负实数，关于x的方程x2﹣（k+1）x+k＝0和kx2﹣（k+2）x+k＝0．

    （1）试证：前一个方程必有两个非负实数根；

    （2）当k取何值时，上述两个方程有一个相同的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P．

    （1）求证：PD是⊙O的切线；

    （2）求证：△PBD∽△DCA；

    （3）当AB=6，AC=8时，求线段PB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某电脑公司有A型，B型，C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元 ，某市实验中学计划将100500元钱全部用于从该电脑公司购进电脑共36台

    （1）若全部购进的是两种不同型号的电脑，请你设计出几种不同的购买方案方案供该校选择，并说出理由;

    （2）能否同时购进三种型号的电脑，若能，请设计出购买方案；若不能，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

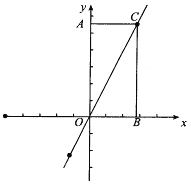
    【题目】有一长方形AOBC纸片放在如图所示的坐标系中，且长方形的两边的比为OA：AC＝2：1.

    （1）求直线OC的解析式；

    （2）求出＝－5时，函数的值；

    （3）求出＝－5时，自变量的值；

    （4）画这个函数的图象；

    （5）根据图象回答，当从2减小到－3时，的值是如何变化的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，三点在同一直线上，.

    （1）已知点在直线上，根据条件，请补充完整图形，并求的长；

    （2）已知点在直线上，分别是，的中点，根据条件，请补充完整图形，并求的长，直接写出与的长存在的数量关系；

    （3）已知点在直线上，分别是，的中点，根据条件，请补充完整图形，并求的长，直接写出与的长存在的数量关系.

    查看答案和解析>>

    同步练习册答案