
【题目】已知某电脑公司有A型,B型,C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元 ,某市实验中学计划将100500元钱全部用于从该电脑公司购进电脑共36台
(1)若全部购进的是两种不同型号的电脑,请你设计出几种不同的购买方案方案供该校选择,并说出理由;
(2)能否同时购进三种型号的电脑,若能,请设计出购买方案;若不能,请说明理由.
【答案】(1)有两种方案供该校选择,第一种方案是购进A型电脑3台和C型电脑33台;第二种方案是购进B型电脑7台和C型电脑29台.(2)不能同时购进三种不同品牌的电脑.
【解析】
(1)分三种情况:一是购买A+B=36,A的单价×数量+B的单价×数量=100500;二是购买A+C=36,A的单价×数量+C的单价×数量=100500;三是购买B+C=36,B的单价×数量+C的单价×数量=100500;
(2)先假设能同时购进三种型号的电脑,列出方程组求解即可.
(1)设从该电脑公司购进A型电脑x台,购进B型电脑y台,购进C型电脑z台,则可分以下三种情况考虑:
(1)只购进A型电脑和B型电脑,依题意可列方程组
![]()
解得![]() .不合题意,应该舍去.
.不合题意,应该舍去.
(2)只购进A型电脑和C型电脑,依题意可列方程组![]()
解得![]() .
.
(3)只购进B型电脑和C型电脑,依题意可列方程组![]()
解得![]() .
.
答:有两种方案供该校选择,第一种方案是购进A型电脑3台和C型电脑33台;
第二种方案是购进B型电脑7台和C型电脑29台.
(2)设从该电脑公司购进A型电脑a台,购进B型电脑b台,购进C型电脑c台,根据题意得,
![]()
消去c得,3500a+1500b=10500
∵a,b均为正整数,
∴a=3,b=0,
∵a+b+c=36,
∴c=33,
故不能同时购进三种型号的电脑.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表:

(1)求a,b的值.
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,求九年级学生可捐助的贫困生中、小学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民1月份用水8m,则应缴费2×6+3×(8-6)+5=23(元)
(1)若用户4月份共用水9.5m3,则需缴费 元;
(2)若该户居民某月缴费54元,则该户居民该月用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,若A、B、C三点满足AC=2CB,则称C是线段AB的相关点.当点C在线段AB上时,称C为线段AB的内相关点,当点C在线段AB延长线上时,称C为线段AB的外相关点.
如图1,当A对应的数为5,B对应的数为2时,则表示数3的点C是线段AB的内相关点,表示数-1的点D是线段AB的外相关点.

(1)如图2,A、B表示的数分别为5和-1,则线段AB的内相关点表示的数为______,线段AB的外相关点表示的数为________.
(2)在(1)的条件下,点P、点Q分别从A点、B点同时出发,点P、点Q分别以3个单位/秒和2个单位/秒的速度向右运动,运动时间为t秒.
①当PQ=7时,求t值.
②设线段PQ的内相关点为M,外相关点为N.直接写出M、N所对应的数为相反数时t的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在y轴右侧且平行于y轴的直线l被反比例函数![]() (
(![]() )与函数
)与函数![]() (
(![]() )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.

【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=![]() (x>0)与函数y=
(x>0)与函数y=![]() +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.

【题型】填空题
【结束】
14
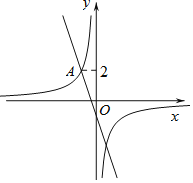
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com