练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

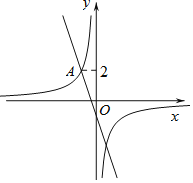
    【题目】如图，在平面直角坐标系xOy中，直线与双曲线相交于点．

    求双曲线的表达式；

    过动点且垂直于x轴的直线与直线及双曲线的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．

    【答案】(1)；（2）或．

    【解析】分析：（1）由点A的坐标利用一次函数图象上点的坐标特征即可求出m值，进而可得出点A的坐标，再由点A的坐标利用待定系数法即可求出双曲线的表达式；
    （2）令，可求出两函数图象交点的横坐标，再根据两函数图象的上下位置关系即可得出当点B位于点C下方时，n的取值范围．

    详解：点在直线上，

    ，

    解得：，

    ．

    点A在双曲线上，

    ，

    双曲线的表达式为．

    令，

    解得：．

    观察函数图象可知：当或时，反比例函数图象在一次函数图象的上方，即点B位于点C下方，

    当点B位于点C下方时，n的取值范围为或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，是由8块棱长都为1的小正方体组合成的简单几何体.

    （1）请画出这个几何体的三视图并用阴影表示出来；

    （2）该几何体的表面积（含下底面）为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，直线AB、CD相交于点O，∠COE＝90°，∠BOD∶∠BOC＝1∶5，过点O作OF⊥AB，则∠EOF的度数为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

    （1）试判断直线BC与⊙O的位置关系，并说明理由；

    （2）若BD=2，BF=2，求阴影部分的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.我们规定，有理数的整数部分就是取其最接近的两个整数中的最小整数，小数部分就是用原数减去整数部分，比如，小数3.25，最接近的两个整数就是3和4，则整数部分取3，小数部分就是3.25-3=0.25，

    （1）3.14的整数部分是 ，小数部分是 ；

    （2）-3.6的整数部分是 ，小数部分是 ；

    （3）如果一个数的整数部分比小数部分大88.11，且整数部分的值恰好是小数部分的100倍，求这个数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知k为非负实数，关于x的方程x2﹣（k+1）x+k＝0和kx2﹣（k+2）x+k＝0．

    （1）试证：前一个方程必有两个非负实数根；

    （2）当k取何值时，上述两个方程有一个相同的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某电脑公司有A型，B型，C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元 ，某市实验中学计划将100500元钱全部用于从该电脑公司购进电脑共36台

    （1）若全部购进的是两种不同型号的电脑，请你设计出几种不同的购买方案方案供该校选择，并说出理由;

    （2）能否同时购进三种型号的电脑，若能，请设计出购买方案；若不能，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用描点法画出函数y=的图象，并回答下列问题：

    (1)当x=-3时， y=_________.

    (2)当1≤x≤4时，y的取值范围是_________.

    查看答案和解析>>

    同步练习册答案