
【题目】已知:如图,直线AB、CD相交于点O,∠COE=90°,∠BOD∶∠BOC=1∶5,过点O作OF⊥AB,则∠EOF的度数为__.

【答案】30°或150°
【解析】
作出图形,分OF、OE在直线AB的同侧或异侧两种情况讨论.根据平角的定义可求∠BOD,根据余角的定义可求∠BOE,根据余角的性质和角的和差关系可求∠EOF或∠EOF'的度数即可.
∵∠BOD:∠BOC=1:5,∠BOD+∠BOC=180°,
∴∠BOD=30°.
∵∠COE=90°,
∴∠DOE=90°,
∴∠BOE=90°-30°=60°.
①若OF、OE在直线AB的同侧.
∵FO⊥AB,
∴∠FOB=90°,
∴∠EOF=∠BOD=30°.
②若OF'、OE在直线AB的同侧.
∵F'O⊥AB,
∴∠F'OB=90°,
∴∠EOF'=∠EOB+∠F'OB=60°+90°=150°.
综上所述:∠EOF的度数为30°或150°.

故答案为:30°或150°.


科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A,且点A到x轴的距离是4.
的图象经过点A,且点A到x轴的距离是4.
(1) 求点A的坐标;
(2) 点![]() 为坐标原点,点
为坐标原点,点![]() 是x轴正半轴上一点,当
是x轴正半轴上一点,当![]() 时,求直线AB的解析式.
时,求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.
(1)求该商场两次共购进多少瓶葡萄酒.
(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).
查看答案和解析>>
科目:初中数学 来源: 题型:
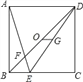
【题目】如图,正方形ABCD中,点E在边BC上,且CE=2BE.连接BD、DE、AE,且AE交BD于F,OG为△BDE的中位线.下列结论:①OG⊥CD;②AB=5OG;③![]() ;④BF=OF;⑤
;④BF=OF;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车都从A地出发,在路程为360千米的同一道路上驶向B地.甲车先出发匀速驶向B地.10分钟后乙车出发,乙车匀速行驶3小时后在途中的配货站装货耗时20分钟.由于满载货物,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时,结果与甲车同时到达B地.
小时,结果与甲车同时到达B地.
(1)甲车的速度为 千米/时;
(2)求乙车装货后行驶的速度;
(3)乙车出发 小时与甲车相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴ ∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.
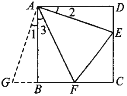
∵ ∠EAF=45°∴ ∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵ ∠1=∠2,∠1+∠3=45°.
即∠GAF=∠________.
又AG=AE,AF=AE
∴ △GAF≌△________.
∴ _________=EF,故DE+BF=EF.
(2)方法迁移:
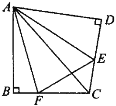
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
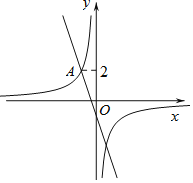
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com