
【题目】用描点法画出函数y=![]() 的图象,并回答下列问题:
的图象,并回答下列问题:
(1)当x=-3时, y=_________.
(2)当1≤x≤4时,y的取值范围是_________.
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在y轴右侧且平行于y轴的直线l被反比例函数![]() (
(![]() )与函数
)与函数![]() (
(![]() )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.

【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=![]() (x>0)与函数y=
(x>0)与函数y=![]() +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.

【题型】填空题
【结束】
14
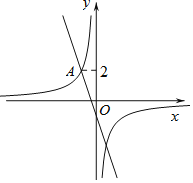
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
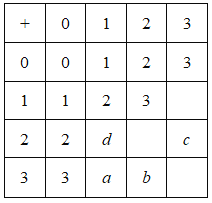
【题目】体育课上的口令:立正,向右转,向后转,向左转之间可以相加.连结执行两个口令就把这两个口令加起来.例如:向右转+向左转=立正;向左转+向后转=向右转.如果分别用0,1,2,3分别代表立正,向右转,向后转,向左转,就可以用如图所示的加法表来表示,在表中填了部分的数值和代表数值的字母.下列对于字母![]() 的值,说法错误的是( )
的值,说法错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:“2_3_5_9”,在每个“____”上,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算“____”上的符号;
,请推算“____”上的符号;
(3)在“2__3__5+9”的“__”上填入符号后,使计算所得数最小,直接写出填上符号后的算式及算式的计算结果的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题1:设a、b是方程x2+x-2012=0的两个实数根,则a2+2a+b的值为________;
问题2:方程x2-2x-1=0的两个实数根分别为x1,x2,则(x1―1)(x2―1)=_______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com