
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

【答案】(1)证明见解析;(2)证明见解析;(3)PB=![]() .
.
【解析】试题分析:(1)由直径所对的圆周角为直角得到∠BAC为直角,再由AD为角平分线,得到一对角相等,根据同弧所对的圆心角等于圆周角的2倍及等量代换确定出∠DOC为直角,与平行线中的一条垂直,与另一条也垂直得到OD与PD垂直,即可得证;
(2)由PD与BC平行,得到一对同位角相等,再由同弧所对的圆周角相等及等量代换得到∠P=∠ACD,根据同角的补角相等得到一对角相等,利用两对角相等的三角形相似即可得证;
(3)由三角形ABC为直角三角形,利用勾股定理求出BC的长,再由OD垂直平分BC,得到DB=DC,根据(2)的相似,得比例,求出所求即可.
试题解析:(1)证明:∵圆心O在BC上,∴BC是圆O的直径,∴∠BAC=90°,连接OD,∵AD平分∠BAC,∴∠BAC=2∠DAC,∵∠DOC=2∠DAC,∴∠DOC=∠BAC=90°,即OD⊥BC,∵PD∥BC,∴OD⊥PD,∵OD为圆O的半径,∴PD是圆O的切线;
(2)证明:∵PD∥BC,∴∠P=∠ABC,∵∠ABC=∠ADC,∴∠P=∠ADC,∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,∴∠PBD=∠ACD,∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,∴BC2=AB2+AC2=62+82=100,∴BC=10,∵OD垂直平分BC,∴DB=DC,∵BC为圆O的直径,∴∠BDC=90°,在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,∴DC=DB=![]() ,∵△PBD∽△DCA,∴
,∵△PBD∽△DCA,∴![]() ,则PB=
,则PB=![]() =
=![]() =
=![]() .
.



 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
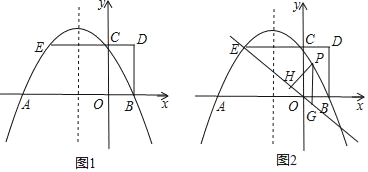
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
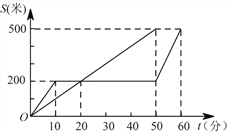
A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
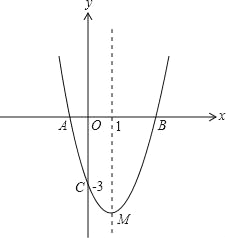
【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
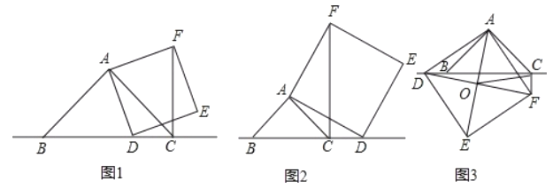
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF. ②![]() .
.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系,
②若连接正方形对角线AE,DF,交点为0,连接OC,探究△AOC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com