
【题目】已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
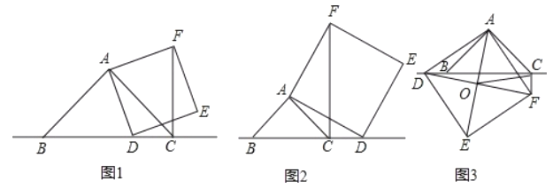
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF. ②![]() .
.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系,
②若连接正方形对角线AE,DF,交点为0,连接OC,探究△AOC的形状,并说明理由.
【答案】(1)①见解析;②见解析;(2)见解析(3)①见解析;②见解析.
【解析】
(1)①根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,再根据正方形的性质可得AD=AF,∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠ACF+∠ACB=90°,从而得证;②根据全等三角形对应边相等可得BD=CF,从而求出CF=BC-CD;
(2)与(1)同理可得BD=CF,然后结合图形可得CF=BC+CD;
(3)①与(1)同理可得BD=CF,然后结合图形可得CF=CD-BC;②根据等腰直角三角形的性质求出∠ABC=∠ACB=45°,再根据邻补角的定义求出∠ABD=135°,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠FCD=90°,然后根据直角三角形斜边上的中线等于斜边的一半求出OC=![]() DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
(1)证明:①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中, 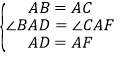
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
②由①△BAD≌△CAF可得BD=CF,
∵BD=BC-CD,
∴CF=BC-CD;
(2)与(1)同理可得BD=CF,
所以,CF=BC+CD;
(3)①与(1)同理可得,BD=CF,
所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAF+∠CAF=90°,
∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,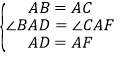
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°,
∴∠FCD=∠ACF-∠ACB=90°,
则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点,
∴OC=![]() DF,
DF,
∵在正方形ADEF中,OA=![]() AE,AE=DF,
AE,AE=DF,
∴OC=OA,
∴△AOC是等腰三角形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
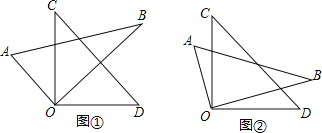
【题目】把一副三角板的直角顶点O重叠在一起.
(1)问题发现:如图①,当OB平分∠COD时,∠AOD+∠BOC的度数是 ;
(2)拓展探究:如图②,当OB不平分∠COD时,∠AOD+∠BOC的度数是多少?
(3)问题解决:当∠BOC的余角的4倍等于∠AOD时,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,点A对应的数为-20,点B对应的数为120.
![]()
(1)请写出线段AB的中点C对应的数.
(2)点P从点B出发,以3个单位/秒的速度向左运动,同时点Q从点A出发,以2个单位/秒的速度向右运动,当点P、Q重合时对应的数是多少?
(3)在(2)的条件下,P、Q两点运动多长时间相距50个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点P每次沿着与x轴成45°的方向运动,第一次从原点O向右上方运动1个单位长度到P1(![]() ,
,![]() ),第二次从点P1向右下方运动1个单位长度到P2(
),第二次从点P1向右下方运动1个单位长度到P2(![]() ,0),第三次从点p2向右下方运动2个单位长度到P3(2
,0),第三次从点p2向右下方运动2个单位长度到P3(2![]() ,-
,-![]() ),第四次从点P3向右上方动2个单位长度到P4(3
),第四次从点P3向右上方动2个单位长度到P4(3![]() ,0),第五次从点P4向右上方运动3个单位长度到P5(
,0),第五次从点P4向右上方运动3个单位长度到P5(![]() ,
,![]() ),第六次从点P5向右下方运动3个单位长度到P6(6
),第六次从点P5向右下方运动3个单位长度到P6(6![]() ,0)……依此规律下去,则P43的坐标为( )
,0)……依此规律下去,则P43的坐标为( )

A. (242![]() ,-11
,-11![]() )B. (242
)B. (242![]() ,11
,11![]() )
)
C. (![]() )D. (
)D. (![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com