
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】:
试题分析:利用思路:知(连)半径,证垂直,证明DE是圆O的切线;利用射影定理或相似三角形证明:BE2=BE×BA,再列方程,求AE的长.
试题解析:(1)如图所示,连接OE,CE
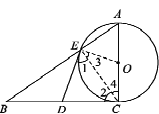
∵AC是圆O的直径
∴∠AEC=∠BEC=90°
∵D是BC的中点
∴ED=![]() BC=DC
BC=DC
∴∠1=∠2
∵OE=OC
∴∠3=∠4
∴∠1+∠3=∠2+∠4,即∠OED=∠ACD
∵∠ACD=90°
∴∠OED=90°,即OE⊥DE
又∵E是圆O上的一点
∴DE是圆O的切线.
(2)由(1)知∠BEC=90°
在RtΔBEC与RtΔBCA中,∠B为公共角,
∴ΔBEC∽ΔBCA
∴![]()
即BC2=BE×BA
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x.
又∵BC=6
∴62=2x×3x
∴x=![]() ,即AE=
,即AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
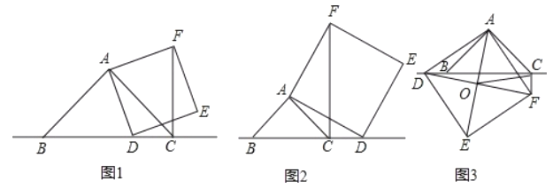
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF. ②![]() .
.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系,
②若连接正方形对角线AE,DF,交点为0,连接OC,探究△AOC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0).
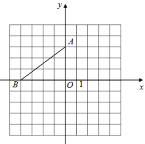
(1)画出△AOB绕点A逆时针旋转90°后得到的图形△A1O1B1;并写出点B1的坐标 ;
(2)画出△AOB关于点P(0,-1)的中心对称图形△A2O2B2,并写出点B2的坐标 ;
(3)若点Q为x轴上的一点,当B1Q+B2 Q的和最小时,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
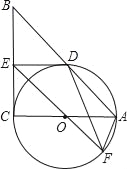
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD两邻边的长m,n是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)求k的取值范围.
(2)当k为何值时,四边形ABCD的两条对角线的长相等,且都等于![]() ,求出这时四边形ABCD的周长和面积.
,求出这时四边形ABCD的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验中学八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
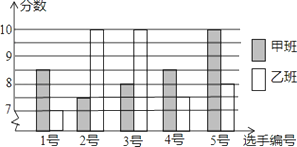
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ______ | ______ |
乙班 | 8.5 | _____ | 10 | 1.6 |
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,E,F是数轴上的点.回答下列问题:

(1)A,C两点间的距离是多少?
(2)若点E与点B的距离是2,则E点表示的数是什么?
(3)F点与A点的距离是m(m>0),F点表示的数是多少?(用含字母m的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com