
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
【答案】A
【解析】分析:当AB=BC时,四边形DBFE是菱形.根据三角形中位线定理证明即可;当BE平分∠ABC时,可证BD=DE,可得四边形DBFE是菱形,当EF=FC,可证EF=BF,可得四边形DBFE是菱形,由此即可判断;
详解:当AB=BC时,四边形DBFE是菱形;
理由:∵点D、E、F分别是边AB、AC、BC的中点,
∴DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∵DE=![]() BC,EF=
BC,EF=![]() AB,
AB,
∴DE=EF,
∴四边形DBFE是菱形.
故B正确,不符合题意,
当BE平分∠ABC时,可证BD=DE,可得四边形DBFE是菱形,
当EF=FC,可证EF=BF,可得四边形DBFE是菱形,
故C、D不符合题意,
故选A.


科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,点A对应的数为-20,点B对应的数为120.
![]()
(1)请写出线段AB的中点C对应的数.
(2)点P从点B出发,以3个单位/秒的速度向左运动,同时点Q从点A出发,以2个单位/秒的速度向右运动,当点P、Q重合时对应的数是多少?
(3)在(2)的条件下,P、Q两点运动多长时间相距50个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大课间是学校的校体课程之一,涉及的范围广,内容繁多。某校根据实际情况决定开设![]() :乒乓球,
:乒乓球,![]() :篮球,
:篮球,![]() :跑步,
:跑步,![]() :跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:
:跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:

(1)补全条形统计图;
(2)制作扇形统计图;
(3)若该校有学生2400人,请问:喜欢打乒乓球的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,某风景区在![]() 天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化 单位:万人 |
|
|
|
|
|
| -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数?
日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2013次输出的结果为( )
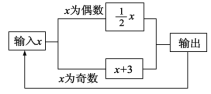
A.6B.3C.![]() D.
D.![]() +3×1003
+3×1003
查看答案和解析>>
科目:初中数学 来源: 题型:
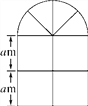
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
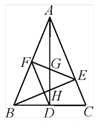
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,BE⊥AC于点E,点F是AB的中点, AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;② AH=2BD; ③AD·BC=AE·AB; ④2CD2=![]() EH2.其中正确的结论有( )
EH2.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com