
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,BE⊥AC于点E,点F是AB的中点, AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;② AH=2BD; ③AD·BC=AE·AB; ④2CD2=![]() EH2.其中正确的结论有( )
EH2.其中正确的结论有( )
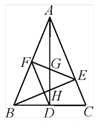
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析:由直角三角形斜边上的中线性质得出FD=![]() AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=
AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=![]() AB,延长FD=FE,①正确;
AB,延长FD=FE,①正确;
证出∠ABC=∠C,得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,得出AH=BC=2CD=2BD,②正确;
证明△ABD~△BCE,得出![]() =
=![]() ,即BCAD=ABBE,③正确;
,即BCAD=ABBE,③正确;
△ABE是等腰直角三角形,得到AB=AC=![]() AE,从而有EC=(
AE,从而有EC=(![]() -1)AE,
-1)AE,
变形得AE= (![]() )EH,变形得
)EH,变形得![]() =
=![]() ,由
,由![]() =
=![]() ,变形即可得到④正确;即可得出结论.
,变形即可得到④正确;即可得出结论.
详解:∵在△ABC中,AD和BE是高,∴∠ADB=∠AEB=∠CEB=90°.
∵点F是AB的中点,∴FD=![]() AB.
AB.
∵∠BAC=45°,∴∠ABE=45°,∴△ABE是等腰直角三角形,∴AE=BE.
∵点F是AB的中点,∴FE=![]() AB,∴FD=FE,①正确;
AB,∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,∴∠ABC=∠C,∴AB=AC.
∵AD⊥BC,∴BC=2CD,∠BAD=∠CAD=∠CBE.在△AEH和△BEC中,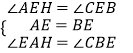 ,∴△AEH≌△BEC(ASA),∴AHBC=2CD=2BD,②正确;
,∴△AEH≌△BEC(ASA),∴AHBC=2CD=2BD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,∴△ABD~△BCE,∴![]() =
=![]() ,即BCAD=ABBE.故③正确;
,即BCAD=ABBE.故③正确;
∵△ABE是等腰直角三角形,∴AB=![]() AE,∴AC=
AE,∴AC=![]() AE,∴EC=(
AE,∴EC=(![]() -1)AE,
-1)AE,
∴AE=![]() EH=(
EH=(![]() )EH,
)EH,![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴2CD2=
,∴2CD2=![]() EH2,故④正确.
EH2,故④正确.
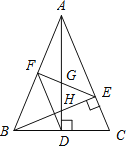
故选D.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
摸到白球的频率 |
| 0.64 | 0.58 |
| 0.60 | 0.601 |
(1)完成上表;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,E,F是数轴上的点.回答下列问题:

(1)A,C两点间的距离是多少?
(2)若点E与点B的距离是2,则E点表示的数是什么?
(3)F点与A点的距离是m(m>0),F点表示的数是多少?(用含字母m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
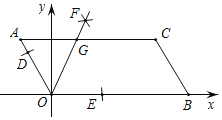
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
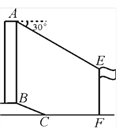
【题目】如图,某学校一教学楼高AB=15米,在它的正前方有一旗杆EF,从教学楼顶端A测得旗杆顶端E的俯角为30°,旗杆低端F到大楼前梯坎底边的距离CF=12米,梯坎坡长BC=6.5米,梯坎坡度i=1:2.4,求旗杆EF的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旗县开展2018美丽乡村美化绿化活动,小康村计划购买垂柳和丁香两种花木共100棵绿化村里的小广场,其中垂柳每棵50元,丁香每棵100元.
(1)若购进垂柳,丁香两种花木刚好用去8000元,则购买了垂柳,丁香两种花木各多少棵?
(2)如果购买丁香的数量不少于垂柳的数量,请你设计一种购买方案,使所需总费用最低,并求出该购买方案所需总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
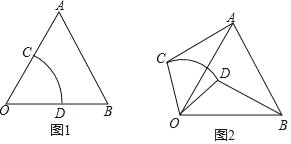
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°)
(1)当OC∥AB时,旋转角α= 度;
发现:(2)线段AC与BD有何数量关系,请仅就图2给出证明.
应用:(3)当A、C、D三点共线时,求BD的长.
拓展:(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com