
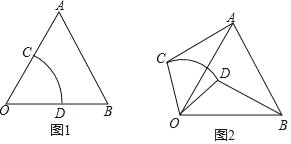
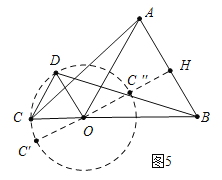
����Ŀ���ڵȱ���AOB�У�������COD��ͼ1�ڷţ�ʹ���εİ뾶OC��OD�ֱ���OA��OB�غϣ�OA=OB=2��OC=OD=1���̶��ȱ���AOB������������COD�Ƶ�O��ʱ����ת���߶�AC��BDҲ��֮�仯������ת��Ϊ������0������360�㣩
��1����OC��ABʱ����ת����=�� ���ȣ�
���֣���2���߶�AC��BD�к�������ϵ�������ͼ2����֤����
Ӧ�ã���3����A��C��D���㹲��ʱ����BD�ij���
��չ����4��P���߶�AB������һ�㣬������COD����ת�����У���ֱ��д���߶�PC�����ֵ����Сֵ��
���𰸡���1��60��240��(2) AC=BD�����ɼ���������3��![]() ��
��![]() ����4��PC�����ֵ=3��PC����Сֵ=
����4��PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��
����������������1����ͼ1������֪����D���߶�AD���߶�AD���ӳ�����ʱ��OC��AB����ʱ��ת����=60����240�㣮
��2��������AC=BD��ֻҪ֤����AOC�ա�BOD���ɣ�
��3����ͼ3��ͼ4�����ֱ���⼴�ɣ�
��4����ͼ5��������������C����OΪԲ����1Ϊ�뾶�ġ�O���˶�������O��OH��AB��H��ֱ��OH����O��C�䡢C�壬�߶�CB�ij���ΪPC�����ֵ���߶�C��H�ij���ΪPC����Сֵ����֪PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��
�������1����ͼ1�У��ߡ�ABC�ǵȱ������������AOB=��COD=60�㣬�൱��D���߶�AD���߶�AD���ӳ�����ʱ��OC��AB����ʱ��ת����=60����240�㣮
�ʴ�Ϊ��60��240��
��2��������AC=BD������������
��ͼ2�У��ߡ�COD=��AOB=60�㣬���COA=��DOB������AOC�͡�BOD����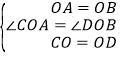 �����AOC�ա�BOD����AC=BD��
�����AOC�ա�BOD����AC=BD��
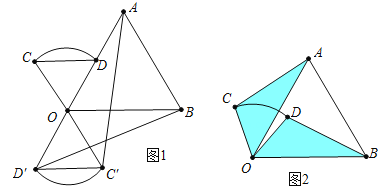
��3������ͼ3������A��C��D����ʱ����OH��AC��H��
��Rt��COH�У���OC=1����COH=30�㣬��CH=HD=![]() ��OH=
��OH=![]() ����Rt��AOH����AH=
����Rt��AOH����AH=![]() =
=![]() ����BD=AC=CH+AH=
����BD=AC=CH+AH=![]() ��
��
��ͼ4������A��C��D����ʱ����OH��AC��H��
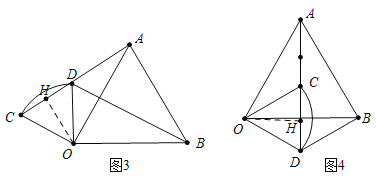
��֪AC=BD=AH��CH=![]() ��
��
������������A��C��D���㹲��ʱ��BD�ij�Ϊ![]() ��
��![]() ��
��
��4����ͼ5��������������C����OΪԲ����1Ϊ�뾶�ġ�O���˶�������O��OH��AB��H��ֱ��OH����O��C�䡢C�壬�߶�CB�ij���ΪPC�����ֵ���߶�C��H�ij���ΪPC����Сֵ����֪PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=45�㣬AD��BC�ڵ�D��BE��AC�ڵ�E����F��AB���е㣬 AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE���� AH=2BD�� ��AD��BC=AE��AB�� ��2CD2=![]() EH2��������ȷ�Ľ�����( )
EH2��������ȷ�Ľ�����( )
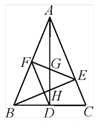
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b(a��0)��ͼ���뷴��������y=![]() (k��0����ͼ����A��B���㣬��x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е㣬AC=4
(k��0����ͼ����A��B���㣬��x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е㣬AC=4![]() ��cos��ACH=
��cos��ACH=![]() ����B������Ϊ(4,n)��
����B������Ϊ(4,n)��

��1����÷�����������һ�κ����Ľ���ʽ��
��2������BCH�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵʱx��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�α�ֱ�����ٹ�·�ϣ��涨�����������ʻ�ٶȲ��ܳ���60km/h����![]() m/s������ͨ������������ù�·100m��������һ�ٶȼ���A������ͼ��ʾ������ϵ�У�Aλ��y���ϣ�����·��BC��x���ϣ���B��A�ı�ƫ��60�������ϣ���C�ڵ�A�ı�ƫ��45�������ϣ�
m/s������ͨ������������ù�·100m��������һ�ٶȼ���A������ͼ��ʾ������ϵ�У�Aλ��y���ϣ�����·��BC��x���ϣ���B��A�ı�ƫ��60�������ϣ���C�ڵ�A�ı�ƫ��45�������ϣ�
��1����ͼ��ֱ�ӱ����ʾ60����45���Ľǣ�
��2��д����B����C���ꣻ
��3��һ�������ӵ�B������ʻ����C����ʱ��Ϊ15s������ͨ�����㣬�жϸ��������������·���Ƿ��٣�����С����![]() ȡ1.7��
ȡ1.7��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A���B�ľ���Ϊ16����λ���ȣ���A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ���B�ڵ�A���Ҳ࣬��C��ʾ�������B��ʾ������Ϊ�෴��������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
��1����A��ʾ����Ϊ________����B��ʾ����Ϊ__________����C��ʾ����Ϊ__________��
��2������P�˶���B��ʱ����Q��A���������ÿ���3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A��
���ڵ�Q���C�˶������У��ܷ��ϵ�P�����ܣ��������Q�˶������ϣ�
���ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ���Ƴ���������ͳ��ͼ��


����������Ϣ�����������������£�
ƽ���ɼ�(��) | ��λ��(��) | ����(��) | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��д��������a��b��c��ֵ��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա������ɼ�����ѡ������һ������������ΪӦѡ������Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
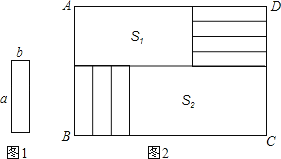
����Ŀ����7����ͬ��С������ֽƬ����ͼ1��ʾ����ͼ2��ʾ�ķ�ʽ���ص��ķ��ڳ�����ABCD�ڣ�δ�����ǵIJ���ǡ�ñ��ָ�Ϊ���������Σ�����ֱ�ΪS1��S2����֪С������ֽƬ�ij�Ϊa����Ϊb����a��b��
�ŵ�a��9��b��3��AD��30ʱ��������ABCD�������������S1��S2��ֵΪ������
�Ƶ�AD��40ʱ�����ú�a��b��ʽ�ӱ�ʾS1��S2��ֵ��
����AB����Ϊ��ֵ��AD�䳤������7��С������ֽƬ������ͬ���ķ�ʽ�����µij�����ABCD�ڣ���S1��S2��ֵ�ܱ��ֲ��䣬��a��b�����ʲô��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���B��60��������ABC�ضԽ���AC�۵�����B�Ķ�Ӧ�����ڵ�E�����ҵ�B��A��E��һ��ֱ���ϣ�CE��AD�ڵ�F����ͼ�еȱ������ι���(����)

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
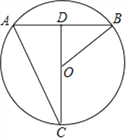
����Ŀ����ͼ����C�ڡ�O�ϣ�����CO���ӳ�����AB�ڵ�D��![]() ������AC��OB����CD=40��AC=
������AC��OB����CD=40��AC=![]() ��
��
��1������AB�ij���
��2����sin��ABO��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com