
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).

(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
(3)直接写出一次函数值大于反比例函数值时x的取值范围.
【答案】(1)![]() ,y=-2x+4;(2)8;(3)x<-2或0<x<4.
,y=-2x+4;(2)8;(3)x<-2或0<x<4.
【解析】分析:(1)首先利用锐角三角函数关系得出HC的长,再利用勾股定理得出AH的长,即可得出A点坐标,进而求出反比例函数解析式,再求出B点坐标,即可得出一次函数解析式;
(2)利用B点坐标的纵坐标再利用HC的长即可得出△BCH的面积.
(3)观察图像可知,在A点左方时:一次函数在反比例函数上方;在B点左方,y轴右方时:一次函数在反比例函数上方,由(1)知点A、点B、的横坐标即可求解.
详解:(1)∵AH⊥x轴于点H,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() ,
,
∴![]() ,
,
解得:HC=4,
∵点O是线段CH的中点,
∴HO=CO=2,
∴AH=![]() =8,
=8,
∴A(-2,8),
∴反比例函数解析式为:![]() ,
,
∴B(4,-4),
∴设一次函数解析式为:y=kx+b,
则![]() ,
,
解得![]() .
.
∴一次函数解析式为:y=-2x+4;
(2)由(1)知:HC=4,B(4,-4),所以△BCH的面积为:![]() ×4×4=8.
×4×4=8.
(3)由(1)知:A(-2,8),B(4,-4).当![]() 时,一次函数在反比例函数上方,所以一次函数值大于反比例函数值时x的取值范围:
时,一次函数在反比例函数上方,所以一次函数值大于反比例函数值时x的取值范围:![]() .
.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
摸到白球的频率 |
| 0.64 | 0.58 |
| 0.60 | 0.601 |
(1)完成上表;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
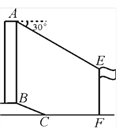
【题目】如图,某学校一教学楼高AB=15米,在它的正前方有一旗杆EF,从教学楼顶端A测得旗杆顶端E的俯角为30°,旗杆低端F到大楼前梯坎底边的距离CF=12米,梯坎坡长BC=6.5米,梯坎坡度i=1:2.4,求旗杆EF的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旗县开展2018美丽乡村美化绿化活动,小康村计划购买垂柳和丁香两种花木共100棵绿化村里的小广场,其中垂柳每棵50元,丁香每棵100元.
(1)若购进垂柳,丁香两种花木刚好用去8000元,则购买了垂柳,丁香两种花木各多少棵?
(2)如果购买丁香的数量不少于垂柳的数量,请你设计一种购买方案,使所需总费用最低,并求出该购买方案所需总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉。例如:
|6+7|= 6+7 ;|6—7|=7- 6;|7-6|=7- 6 ;|―6―7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=________;
(2)|![]() |=________;
|=________;
(3)|![]() |=_______;
|=_______;
(4)用合理的方法计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定理中,没有逆定理的是( )
A. 直角三角形的两锐角互余
B. 全等三角形的对应角相等
C. 互为相反数的两数之和为 0
D. 若三角形的三边长 a, b, c 满足 ![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
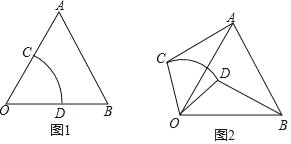
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°)
(1)当OC∥AB时,旋转角α= 度;
发现:(2)线段AC与BD有何数量关系,请仅就图2给出证明.
应用:(3)当A、C、D三点共线时,求BD的长.
拓展:(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联商场预测某品牌村衫能畅销市场,先用了8万元购入这种衬衫,面市后果然供不应求,于是商场又用了17.6万元购入第二批这种衬衫,所购数量是第一批购入量的2倍,但单价贵了4元.商场销售这种衬衫时每件定价都是58元,最后剩下的150件按定价的八折销售,很快售完.
(1)第一次购买这种衬衫的单价是多少?
(2)在这两笔生意中,华联商场共赢利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com