
【题目】华联商场预测某品牌村衫能畅销市场,先用了8万元购入这种衬衫,面市后果然供不应求,于是商场又用了17.6万元购入第二批这种衬衫,所购数量是第一批购入量的2倍,但单价贵了4元.商场销售这种衬衫时每件定价都是58元,最后剩下的150件按定价的八折销售,很快售完.
(1)第一次购买这种衬衫的单价是多少?
(2)在这两笔生意中,华联商场共赢利多少元?
【答案】(1)第一批购入衬衫的单价为每件40元.(2)两笔生意中华联商场共赢利90260元.
【解析】
试题(1)设第一批购入的衬衫单价为x元/件,根据题目中的等量关系“第一批衬衫的数量×2=第二批衬衫的数量”可列方程![]() ,解方程即可.(2)在(1)的基础上可求出两次进货的数量以及每件的单价,在这两笔生意中,华联商场共赢利分三部分,第一批衬衫的盈利和第二批衬衫两部分的盈利,根据每件利润×件数=总利润分别求出这三部分的盈利相加即可得在这两笔生意中,华联商场共赢利的钱数.
,解方程即可.(2)在(1)的基础上可求出两次进货的数量以及每件的单价,在这两笔生意中,华联商场共赢利分三部分,第一批衬衫的盈利和第二批衬衫两部分的盈利,根据每件利润×件数=总利润分别求出这三部分的盈利相加即可得在这两笔生意中,华联商场共赢利的钱数.
试题解析:(1)设第一批购入的衬衫单价为x元/件,根据题意得,
![]() .
.
解得:x=40,经检验x=40是方程的解,
答:第一批购入衬衫的单价为每件40元.
(2)由(1)知,第一批购入了80000÷40=2000件.
在这两笔生意中,华联商场共赢利为:2000×(58﹣40)+(2000×2-150)×(58﹣44)+150×(58×0.8﹣44)=90260元.
答:两笔生意中华联商场共赢利90260元.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).

(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
(3)直接写出一次函数值大于反比例函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
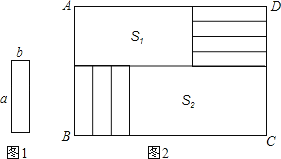
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
⑴当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S1﹣S2的值为 .
⑵当AD=40时,请用含a、b的式子表示S1﹣S2的值;
⑶若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S1﹣S2的值总保持不变,则a、b满足的什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
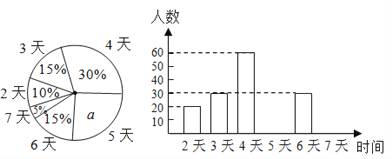
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校初一学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)在这次抽样调查中,众数和中位数分别是多少?
(5)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com