
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
【答案】解:(1)∴x趟,则乙车单独运完此堆垃圾需运2x趟,根据题意得出:
![]() ,
,
解得:x=18,则2x=36。
经检验得出:x=18是原方程的解。
答:甲车单独运完需18趟,乙车单独运完需36趟;
(2)设甲车每一趟的运费是a元,由题意得:
12a+12(a﹣200)=4800,
解得:a=300。
则乙车每一趟的费用是:300﹣200=100(元),
单独租用甲车总费用是:18×300=5400(元),
单独租用乙车总费用是:36×100=3600(元)。
∵3600<5400,故单独租用一台车,租用乙车合算。
【解析】(1)设甲车单独运完此堆垃圾需运x趟,则乙车单独运完此堆垃圾需运2x趟,根据总工作效率![]() 得出等式方程求出即可。
得出等式方程求出即可。
(2)分别表示出甲、乙两车单独运每一趟所需费用,再根据关键语句“两车各运12趟可完成,需支付运费4800元”可得方程,再解出方程,再分别计算出利用甲或乙所需费用进行比较即可。


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画 ![]() ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 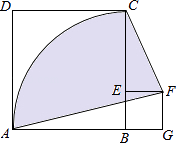
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.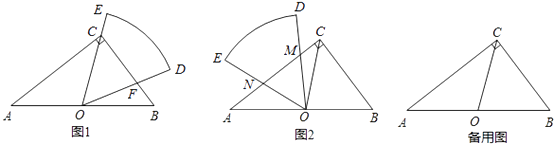
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为 . 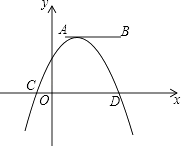
查看答案和解析>>
科目:初中数学 来源: 题型:
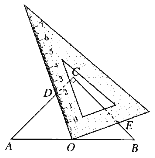
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,边AC的长为![]() ,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值
,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′,利用网格点画图和无刻度的直尺画图并解答(保留画图痕迹):
(1)画出△A′B′C′;
(2)画出△ABC的高,即线段BD;
(3)连接AA′、 CC′,那么AA′与CC′的关系是________;线段AC扫过图形的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.

(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com