练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画 ，连结AF，CF，则图中阴影部分面积为 ．

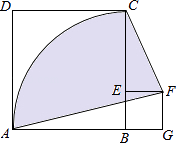
    【答案】4π
    【解析】解：设正方形EFGB的边长为a，则CE=4﹣a，AG=4+a，

    阴影部分的面积=S扇形ABC+S正方形EFGB+S△CEF﹣S△AGF

    = +a2+ a（4﹣a）﹣ a（4+a）

    =4π+a2+2a﹣ a2﹣2a﹣ a2

    =4π．

    所以答案是：4π．

    【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学期即将结束，为了表彰优秀，班主任王老师用W元钱购买奖品．若以2支钢笔和3本笔记本为一份奖品，则可买60份奖品；若以2支钢笔和6本笔记本为一份奖品，则可以买40份奖品．设钢笔单价为x元/支，笔记本单价为y元/本．

    （1）请用y的代数式表示x．

    （2）若用这W元钱全部购买笔记本，总共可以买几本？

    （3）若王老师用这W元钱恰好能买30份同样的奖品，可以选择a支钢笔和b本笔记本作为一份奖品（两种奖品都要有）．请求出所有可能的a，b值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，随着我市铁路建设进程的加快，现规划从A地到B地有一条笔直的铁路通过，但在附近的C处有一大型油库，现测得油库C在A地的北偏东60°方向上，在B地的西北方向上，AB的距离为250（ +1）米．已知在以油库C为中心，半径为200米的范围内施工均会对油库的安全造成影响．问若在此路段修建铁路，油库C是否会受到影响？请说明理由．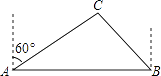

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嘉淇准备完成题目：化简：，发现系数“”印刷不清楚．

    （1）他把“”猜成3，请你化简：（3x2+6x+8）–（6x+5x2+2）；

    （2）他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm．

    （1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？

    （2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．

    （3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，问几秒后，△PBQ的面积为1？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

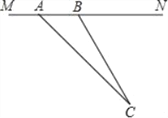
    【题目】“为了安全，请勿超速”，如图所示是一条已经建成并通车的公路，且该公路的某直线路段MN上限速17m/s，为了检测来往车辆是否超速，交警在MN旁设立了观测点C．若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200m．

    （1）求观测点C到公路MN的距离；

    （2）请你判断该汽车是否超速？（参考数据：≈1.41，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

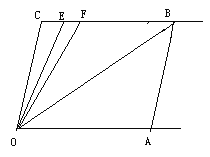
    【题目】如图，直线CB∥OA，∠C=∠A=120°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．

    （1）求∠EOB的度数；

    （2）若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；

    （3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热[此过程中水温y（℃）与开机时间x（分）满足一次函数关系]，当加热到100℃时自动停止加热，随后水温开始下降[此过程中水温y（℃）与开机时间x（分）成反比例关系]，当水温降至20℃时，饮水机又自动开始加热…，重复上述程序（如图所示），根据图中提供的信息，解答下列问题：

    （1）当0≤x≤8时，求水温y（℃）与开机时间x（分）的函数关系式；

    （2）求图中t的值；

    （3）若小明在通电开机后即外出散步，请你预测小明散步45分钟回到家时，饮水机内的温度约为多少℃？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    （1）求甲、乙两车单独运完此堆垃圾各需运多少趟？

    （2）若单独租用一台车，租用哪台车合算？

    查看答案和解析>>

    同步练习册答案