
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
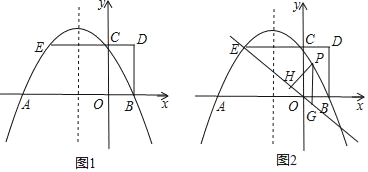
【答案】(1)抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+2;(2)l=﹣
x+2;(2)l=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,![]() ;(3)(2,﹣
;(3)(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() )或(﹣2,2).
)或(﹣2,2).
【解析】试题分析:(1)由条件可求得A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)可先求得E点坐标,从而可求得直线OE解析式,可知∠PGH=45°,用m可表示出PG的长,从而可表示出l的长,再利用二次函数的性质可求得其最大值;
(3)分AC为边和AC为对角线,当AC为边时,过M作对称轴的垂线,垂足为F,则可证得△MFN≌△AOC,可求得M到对称轴的距离,从而可求得M点的横坐标,可求得M点的坐标;当AC为对角线时,设AC的中点为K,可求得K的横坐标,从而可求得M的横坐标,代入抛物线解析式可求得M点坐标.
试题解析:(1)∵矩形OBDC的边CD=1,∴OB=1,∵AB=4,∴OA=3,∴A(﹣3,0),B(1,0),把A、B两点坐标代入抛物线解析式可得:![]() ,解得:
,解得: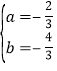 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)在![]() 中,令y=2可得2=
中,令y=2可得2=![]() ,解得x=0或x=﹣2,∴E(﹣2,2),∴直线OE解析式为y=﹣x,由题意可得P(m,
,解得x=0或x=﹣2,∴E(﹣2,2),∴直线OE解析式为y=﹣x,由题意可得P(m,![]() ),∵PG∥y轴,∴G(m,﹣m),∵P在直线OE的上方,∴PG=
),∵PG∥y轴,∴G(m,﹣m),∵P在直线OE的上方,∴PG=![]() ﹣(﹣m)=
﹣(﹣m)=![]() =
=![]() ,∵直线OE解析式为y=﹣x,∴∠PGH=∠COE=45°,∴l=
,∵直线OE解析式为y=﹣x,∴∠PGH=∠COE=45°,∴l=![]() PG=
PG=![]() [
[![]() ]=
]=![]() ,∴当m=
,∴当m=![]() 时,l有最大值,最大值为
时,l有最大值,最大值为![]() ;
;
(3)①当AC为平行四边形的边时,则有MN∥AC,且MN=AC,如图,过M作对称轴的垂线,垂足为F,设AC交对称轴于点L,则∠ALF=∠ACO=∠FNM,在△MFN和△AOC中,∵∠MFN=∠AOC,∠FNM=∠ACO,MN=AC,∴△MFN≌△AOC(AAS),∴MF=AO=3,∴点M到对称轴的距离为3,又![]() ,∴抛物线对称轴为x=﹣1,设M点坐标为(x,y),则|x+1|=3,解得x=2或x=﹣4,当x=2时,y=﹣
,∴抛物线对称轴为x=﹣1,设M点坐标为(x,y),则|x+1|=3,解得x=2或x=﹣4,当x=2时,y=﹣![]() ,当x=﹣4时,y=
,当x=﹣4时,y=![]() ,∴M点坐标为(2,﹣
,∴M点坐标为(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() );
);
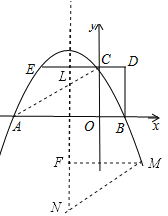
②当AC为对角线时,设AC的中点为K,∵A(﹣3,0),C(0,2),∴K(﹣![]() ,1),∵点N在对称轴上,∴点N的横坐标为﹣1,设M点横坐标为x,∴x+(﹣1)=2×(﹣
,1),∵点N在对称轴上,∴点N的横坐标为﹣1,设M点横坐标为x,∴x+(﹣1)=2×(﹣![]() )=﹣3,解得x=﹣2,此时y=2,∴M(﹣2,2);
)=﹣3,解得x=﹣2,此时y=2,∴M(﹣2,2);
综上可知点M的坐标为(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() )或(﹣2,2).
)或(﹣2,2).


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,且
,且![]() .
.
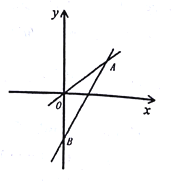
(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的面积为32,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交BC,AD于点E、F,若AF=3DF,则图中阴影部分的面积等于_____

查看答案和解析>>
科目:初中数学 来源: 题型:
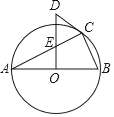
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
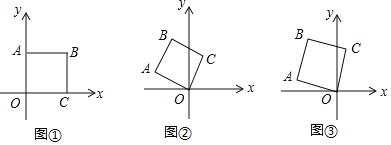
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com