
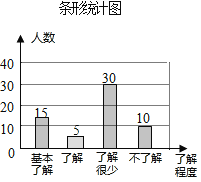
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
【答案】(1)60,90°(2)5(3)![]()
【解析】试题分析:(1)根据了解很少的人数和所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角
的度数;
(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;
(3)根据题意先画出树状图,再根据概率公式即可得出答案.
试题解析:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人).
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为: ![]() ×360°=90°.
×360°=90°.
(2)了解的人数有:60-15-30-10=5(人),补图如下:
(3)画树状图得:
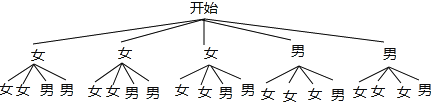
∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为: ![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+
x2+![]() x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD.设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD.设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示. 
(1)求甲车从A地到达B地所用的时间为;
(2)求出甲车返回A地时y与x函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 表示的数为
表示的数为![]() ,
, ![]() ,
, ![]() .
.
(![]() )写出数轴上点
)写出数轴上点![]() 、
、![]() 表示的数:__________,__________.
表示的数:__________,__________.
(![]() )动点
)动点![]() ,
, ![]() 同时从
同时从![]() ,
, ![]() 出发,点
出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以
以![]() 个单位长度的速度沿数向左匀速运动,设运动时间为
个单位长度的速度沿数向左匀速运动,设运动时间为![]() 秒.
秒.
①求数轴上点![]() ,
, ![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,点
为何值时,点![]() ,
, ![]() 相距
相距![]() 个单位长度.
个单位长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com