
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
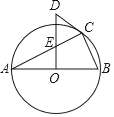
【答案】(1)证明见解析;(2)∠CDE=2∠A,理由见解析.
【解析】分析:(1)由勾股定理求AB,证明△AOE∽△ACB,根据相似三角形的对应线段成比例求OE;(2)连接OC,可知∠3=2∠A,只需用同角的余角证∠D=∠3即可.
详解:(1)∵AB为⊙O的直径,∴∠ACB=900,
在Rt△ABC中,由勾股定理得:AB=![]() =3
=3![]() ,
,
∴OA=![]() AB=
AB=![]() .
.
∵OD⊥AB,∴∠AOE=∠ACB=900,由∵∠A=∠A,∴△AOE∽△ACB,
∴![]() ,即
,即![]() ,解得:OE=
,解得:OE=![]() .
.
(2)∠CDE=2∠A,
理由如下:连接OC,如图所示:
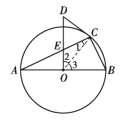
∵OA=OC,∴∠1=∠A,
∵CD是⊙O的切线,∴OC⊥CD,∴∠OCD=900,∴∠2+∠CDE=900,
∵OD⊥AB,∴∠2+∠3=900,∴∠3=∠CDE,∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.


科目:初中数学 来源: 题型:
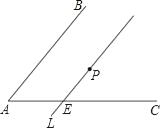
【题目】如图,∠BAC内有一点P,过点P作直线l∥AB,交AC于E点.今欲在∠BAC的两边上各找一点Q、R,使得P为QR的中点,以下是甲、乙两人的作法:
甲:①过P作直线l1∥AC,交直线AB于F点,并连接EF;
②过P作直线l2∥EF,分别交两直线AB、AC于Q、R两点,则Q、R即为所求.
乙:①在直线AC上另取一点R,使得AE=ER;
②作直线PR,交直线AB于Q点,则Q、R即为所求.
下列判断正确的是( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
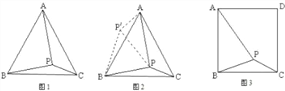
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
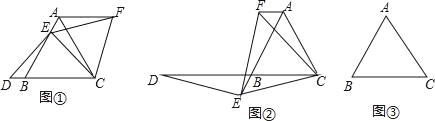
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
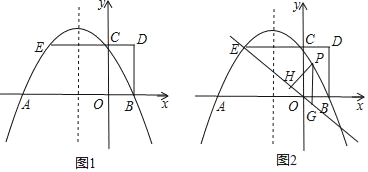
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“*”表示一种新运算:对于任意正实数a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
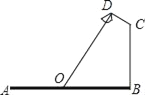
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com