
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,且
,且![]() .
.
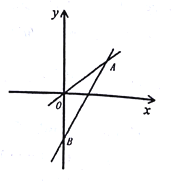
(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)(+12)﹣(﹣7)+(﹣5)﹣(+30)
(2)![]()
(3)﹣33×(﹣2)﹣12÷[(﹣3)﹣(﹣1)]
(4)(﹣![]() )×(﹣3)3﹣0.25×(﹣3)×(﹣2)4
)×(﹣3)3﹣0.25×(﹣3)×(﹣2)4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B.当点M在y=
的图象于点B.当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( )
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取;乙商场规定:凡超过
收取;乙商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取.某顾客购买的电器价格是
收取.某顾客购买的电器价格是 ![]() 元.
元.
(1)当 ![]() 时,该顾客应选择在 商场购买比较合算;
时,该顾客应选择在 商场购买比较合算;
(2)当 ![]() 时,分别用代数式表示在两家商场购买电器所需付的费用;
时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当 ![]() 时,该顾客应选择哪一家商场购买比较合算?说明理由.
时,该顾客应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是药品研究所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物浓度至少需要多长时间达到最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC内有一点P,过点P作直线l∥AB,交AC于E点.今欲在∠BAC的两边上各找一点Q、R,使得P为QR的中点,以下是甲、乙两人的作法:
甲:①过P作直线l1∥AC,交直线AB于F点,并连接EF;
②过P作直线l2∥EF,分别交两直线AB、AC于Q、R两点,则Q、R即为所求.
乙:①在直线AC上另取一点R,使得AE=ER;
②作直线PR,交直线AB于Q点,则Q、R即为所求.
下列判断正确的是( )
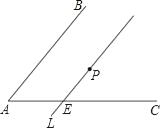
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
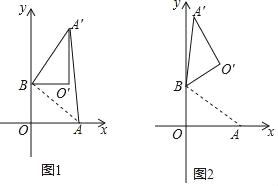
【题目】在平面直角坐标系中,O为原点,点A(8,0),点B(0,6),把△ABO绕点B逆时针旋转得△A′B′O′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
(1)如图1,若α=90°,则AB= ,并求AA′的长;
(2)如图2,若α=120°,求点O′的坐标;
(3)在(2)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,直接写出点P′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
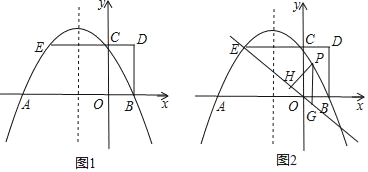
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com