
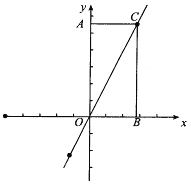
【题目】有一长方形AOBC纸片放在如图所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出![]() =-5时,函数
=-5时,函数![]() 的值;
的值;
(3)求出![]() =-5时,自变量
=-5时,自变量![]() 的值;
的值;
(4)画这个函数的图象;
(5)根据图象回答,当![]() 从2减小到-3时,
从2减小到-3时,![]() 的值是如何变化的?
的值是如何变化的?
 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论: ①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CEAB.
其中正确结论的序号是(在横线上填上你认为所有正确结论的代号).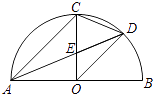
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一个点从数轴上的原点开始,先向左移动7cm到达A点,再从A点向右移动12cm到达B点,把点A到点B的距离记为AB,点C是线段AB的中点.
(1)点C表示的数是_____;
(2)若点A以每秒2cm的速度向左移动,同时C、B点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①点C表示的数是_____(用含有t的代数式表示);
②当t=2秒时,求CB﹣AC的值;
③试探索:CB﹣AC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的图象(折线![]() )描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为![]() 千米/时;
千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管道每小时排水8![]() ,6 h可将满池水全部排空.
,6 h可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管道,使 每小时的排水量达到Q(![]() ),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.
),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.
(3)如果准备在5h内将满池水排空,那第每小时排水量到少为多少?
(4)已知排水管的最大排水量为每小时12![]() ,那么最少多长时间可将满池水全部排空?
,那么最少多长时间可将满池水全部排空?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有小时.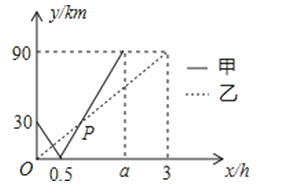
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形.请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com