
����Ŀ��ij��ˮ�ص���ˮ�ܵ�ÿСʱ��ˮ8![]() ,6 h�ɽ�����ˮȫ���ſգ�
,6 h�ɽ�����ˮȫ���ſգ�
��1����ˮ�ص��ݻ��Ƕ��٣�
��2�����������ˮ�ܵ���ʹ ÿСʱ����ˮ���ﵽQ(![]() )��������ˮ�ſ�����ʱ��Ϊt(h)����Q��t֮��ĺ�����ϵʽ��
)��������ˮ�ſ�����ʱ��Ϊt(h)����Q��t֮��ĺ�����ϵʽ��
��3���������5h�ڽ�����ˮ�ſգ�����ÿСʱ��ˮ������Ϊ���٣�
��4����֪��ˮ�ܵ������ˮ��ΪÿСʱ12![]() ����ô���ٶʱ��ɽ�����ˮȫ���ſգ�
����ô���ٶʱ��ɽ�����ˮȫ���ſգ�
���𰸡���1��48![]() ��2��
��2��![]() ��3��9.6
��3��9.6![]() ��4��������5h�ɽ�����ˮȫ���ſ�
��4��������5h�ɽ�����ˮȫ���ſ�
�����������������ݣ�ÿСʱ��ˮ������ˮʱ��=��ˮ�ص��ݻ������Եõ�������ϵʽ��
��1����֪ÿСʱ��ˮ��8m2����ˮʱ��6h��������ˮ�ص��ݻ�Ϊ48m3��
��2����![]() �ɵã�
�ɵã�![]() .
.
��3����4�����Ǻ�����ϵʽ�����ã�
��⣺(1)��ˮ�ص��ݻ��ǣ�8��6=48(![]() )��
)��
(2)t��Q֮��Ĺ�ϵʽΪ![]() ��
��
(3)��![]() ,�ⲻ��ʽ��,Q
,�ⲻ��ʽ��,Q![]() 9.6,��ÿСʱ����ˮ������Ϊ9.6
9.6,��ÿСʱ����ˮ������Ϊ9.6![]() ��
��
(4)��Q=12ʱ����Q��t=48��t=4����������4h�ɽ�����ˮȫ���ſ�.


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ���ʾ�ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף�����ijʳƷ��Ϊ�˽������ȥ�����۽Ϻõ������ء���ɳ���ա��������ա��������գ����·ֱ���A��B��C��D��ʾ�������ֲ��ÿ�ζ���ӵ�ϲ��������ڽ�ǰ��ij�����������˳������飬��������������Ƴ���������ͳ��ͼ���в��������� 
�����������Ϣ�ش�
��1�����βμӳ�������ľ����ж����ˣ�
��2����������������ͼ����������
��3������������8000�ˣ�����ư���D�յ�������
��4������������ȫ��ͬ��A��B��C��D�ո�һ���������С���������������б�����״ͼ�ķ����������ڶ���ǡ�óԵ�����C�յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ��˾��ij������һ��ţ�̣�����·����ÿǧ�����˷�0.60Ԫ���ɹ�·���䣬ÿǧ�����˷�0.30Ԫ�����貹��600Ԫ
��1����ù�˾���������ţ��Ϊxǧ�ˣ�ѡ����·����ʱ�������˷�Ϊy1Ԫ��ѡ��·����ʱ�������˷�Ϊy2Ԫ����ֱ�д��y1��y2��x֮��Ĺ�ϵʽ��
��2������˾ֻ֧���˷�1500Ԫ����ѡ���������䷽ʽ���͵�ţ�̶ࣿ����˾����1500ǧ��ţ�̣���ѡ���������䷽ʽ������ý��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨��[x]��ʾ������x�������������x����ʾ��С��x����С������[x����ʾ��ӽ�x��������x��n+0.5��nΪ�����������磺[2.3]=2����2.3��=3��[2.3��=2������1��x��1ʱ������ [x]+��x��+[x���Ľ����__________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
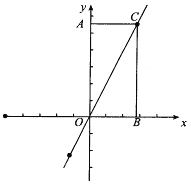
����Ŀ����һ������AOBCֽƬ������ͼ��ʾ������ϵ�У��ҳ����ε����ߵı�ΪOA��AC��2��1.
��1����ֱ��OC�Ľ���ʽ��
��2�����![]() ����5ʱ������
����5ʱ������![]() ��ֵ��
��ֵ��
��3�����![]() ����5ʱ���Ա���
����5ʱ���Ա���![]() ��ֵ��
��ֵ��
��4�������������ͼ��
��5������ͼ��ش𣬵�![]() ��2��С����3ʱ��
��2��С����3ʱ��![]() ��ֵ����α仯�ģ�
��ֵ����α仯�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD���ڵ�O����OBΪֱ����ԲM����D����M�����ߣ��е�ΪN���ֱ�AC��BC�ڵ�E��F����֪AE=5��CE=3����DF�ij��ǣ�������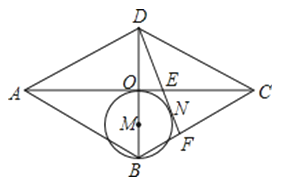
A.3
B.4
C.4.8
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
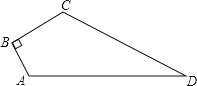
����Ŀ����ͼ����֪�ı���ABCD�У���B=90�㣬AB=3��BC=4��CD=12��AD=13�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��AD=6��P��Q�ֱ���AB��CD�ϵ�����һ�㣬��AP=CQ���߶�EF��PQ�Ĵ�ֱƽ���ߣ���BC��F����PQ��E����AP=x��BF=y����y��x�ĺ�����ϵʽΪ ��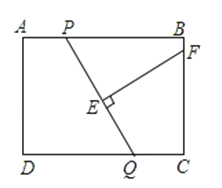
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��߷�չ��С���ƻ������ѿ��һ������Ʒ�����˽��м������ҿ�ݹ�˾�ȽϺ��ʣ���˾��ʾ�������Ʒ������![]() ǧ�˵ģ���ÿǧ��
ǧ�˵ģ���ÿǧ��![]() Ԫ�շѣ�����
Ԫ�շѣ�����![]() ǧ�ˣ������IJ��ְ�ÿǧ��
ǧ�ˣ������IJ��ְ�ÿǧ��![]() Ԫ�շѣ���С�������Ʒ
Ԫ�շѣ���С�������Ʒ![]() ǧ�ˣ�
ǧ�ˣ�
![]() �ú���
�ú���![]() �Ĵ���ʽ��ʾС�������Ʒ�ķ��ã�
�Ĵ���ʽ��ʾС�������Ʒ�ķ��ã�
![]() ��С�������Ʒ
��С�������Ʒ![]() ǧ�ˣ�Ӧ����ݷѶ���Ԫ��
ǧ�ˣ�Ӧ����ݷѶ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com