
【题目】如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为 .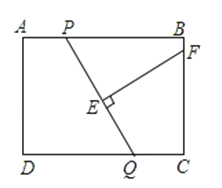
【答案】y=![]() x﹣
x﹣![]()
【解析】解:连接PF,QF,
∵线段EF是PQ的垂直平分线,
∴PF=QF,
∵在矩形ABCD中,AB=8,AD=6,
∴BC=AD=6,
∵AP=x,BF=y,
∴PB=8﹣x,CF=6﹣y,
∵CQ=AP=x,
∴在Rt△PBF中,PF2=PB2+BF2=(8﹣x)2+y2 , 在Rt△CQF中,QF2=CF2+CQ2=(6﹣y)2+x2 ,
∴(8﹣x)2+y2=(6﹣y)2+x2 ,
即y=![]() x﹣
x﹣![]() .
.
故答案为:y=![]() x﹣
x﹣![]() .
. 
首先连接PF,QF,由线段EF是PQ的垂直平分线,可得PF=QF,又由在矩形ABCD中,AB=8,AD=6,AP=x,BF=y,且AP=CQ,可得方程:(8﹣x)2+y2=(6﹣y)2+x2 , 继而求得答案.


科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=4![]() , 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为
, 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管道每小时排水8![]() ,6 h可将满池水全部排空.
,6 h可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管道,使 每小时的排水量达到Q(![]() ),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.
),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.
(3)如果准备在5h内将满池水排空,那第每小时排水量到少为多少?
(4)已知排水管的最大排水量为每小时12![]() ,那么最少多长时间可将满池水全部排空?
,那么最少多长时间可将满池水全部排空?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校大礼堂第一排有![]() 个座位,后面每一排都比前一排多
个座位,后面每一排都比前一排多![]() 个座位,
个座位,
![]() 求第
求第![]() 排的座位数?
排的座位数?
![]() 若该礼堂一共有
若该礼堂一共有![]() 排座位,且第一排的座位数也是
排座位,且第一排的座位数也是![]() ,请你计算一下该礼堂能容纳多少人?
,请你计算一下该礼堂能容纳多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
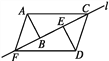
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,
从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照规律填上所缺的单项式并回答问题:
(1)a、﹣2a2、3a3、﹣4a4, , ;
(2)试写出第2007个单项式 ;第2008个单项式 ;
(3)试写出第n个单项式 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com