
【题目】如图,在△BDE中,∠BDE=90°,BD=4![]() , 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为
, 点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 
【答案】(3,2![]() )
)
【解析】解:如图,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F.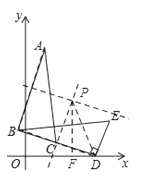
∵点C在BD上,
∴点P到AB、BD的距离相等,都是![]() BD,即
BD,即![]() ×4
×4![]() =2
=2![]() ,
,
∴∠PDB=45°,
PD=![]() ×2
×2![]() =4,
=4,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=![]() PD=
PD=![]() ×4=2,
×4=2,
∵点D的坐标是(5,0),
∴OF=OD﹣DF=5﹣2=3,
由勾股定理得,PF=![]()
∴旋转中心的坐标为(3,2![]() ).
).
故答案为:(3,2![]() ).
).
根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=![]() PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上.
(1)将![]() ABC绕着点B顺时针旋转
ABC绕着点B顺时针旋转![]() ,得到
,得到![]() A1B1C1.
A1B1C1.
(2)画出![]() ABC关于原点的对称图形
ABC关于原点的对称图形![]() A2B2C2
A2B2C2
(3)若点P(a,b)是![]() ABC边上的任意一点,则P关于原点对称的点Q坐标为_______.(用含a,b的式子表示)
ABC边上的任意一点,则P关于原点对称的点Q坐标为_______.(用含a,b的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )

A. ①③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为 .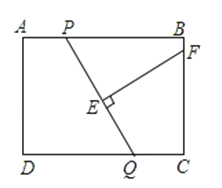
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com