
【题目】已知,一个点从数轴上的原点开始,先向左移动7cm到达A点,再从A点向右移动12cm到达B点,把点A到点B的距离记为AB,点C是线段AB的中点.
(1)点C表示的数是_____;
(2)若点A以每秒2cm的速度向左移动,同时C、B点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①点C表示的数是_____(用含有t的代数式表示);
②当t=2秒时,求CB﹣AC的值;
③试探索:CB﹣AC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)﹣1 0
【解析】
(1)由题意得A点表示的数为﹣7,B点表示的数为5,求出AB的长度,进而求出AC的长度,即可求出点C表示的数;(2)①用含t的代数式表示出C点即可;②分别求出t=2时CB、AC的长度,进而求出CB﹣AC的值;③用含t的式子分别表示出A、B、C三个点,进而表示出CB、AC的长度,计算出CB﹣AC的值即可判断是否变化.
(1)由题意可得:A点表示的数为﹣7,B点表示的数为5,
∴AB=12,
∴AC=12×![]() =6,
=6,
∴点C表示的数为:﹣7+6=﹣1,
故答案为:﹣1;
(2)①由题意可得,
点C移动t秒时表示的数为:﹣1+t,
故答案为:﹣1+t;
②当t=2时,A点表示的数为﹣7﹣2×2=﹣11,
B点表示的数为5+4×2=13,
C点表示的数为﹣1+1×2=1,
∴CB=12,AC=12,
∴CB﹣AC=0;
③CB﹣AC的值不随着时间t的变化而改变,
A点表示的数为﹣7﹣2t,
B点表示的数为5+4t,
C点表示的数为﹣1+t,
∴CB=5+4t﹣(﹣1+t)=6+3t,
AC=﹣1+t﹣(﹣7﹣2t)=6+3t,
∴CB﹣AC=0,
∴CB﹣AC的值不随着时间t的变化而改变,CB﹣AC的值为0cm.


科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )

A. ①③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
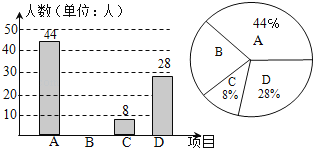
【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼.某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校最喜欢足球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
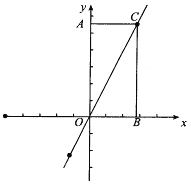
【题目】有一长方形AOBC纸片放在如图所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出![]() =-5时,函数
=-5时,函数![]() 的值;
的值;
(3)求出![]() =-5时,自变量
=-5时,自变量![]() 的值;
的值;
(4)画这个函数的图象;
(5)根据图象回答,当![]() 从2减小到-3时,
从2减小到-3时,![]() 的值是如何变化的?
的值是如何变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com