
【题目】已知如图,![]() 三点在同一直线上,
三点在同一直线上,![]() .
.
(1)已知点![]() 在直线
在直线![]() 上,根据条件,请补充完整图形,并求
上,根据条件,请补充完整图形,并求![]() 的长;
的长;
![]()
(2)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系;
的长存在的数量关系;
![]()
(3)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系.
的长存在的数量关系.
![]()
【答案】(1)图见解析;AC=4或8;(2)图见解析;MN=2或4;MN=![]() ;(3)MN=3;MN=
;(3)MN=3;MN=![]() .
.
【解析】
(1)根据点C的位置有两种情况分类讨论,①当点C在点B的左侧时,易求此时AC的长;②当点C在点B的右侧时,易求此时AC的长;
(2)①当点C在点B的左侧时,根据中点的定义,可得:MB=![]() ,NB=
,NB=![]() ,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
(3)①当点C在点B的左侧时,根据中点的定义,可得:MC=![]() ,CN=
,CN=![]() ,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
解:(1)根据题意,点C的位置有两种情况
①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB-BC=4;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB+BC=8.
综上所述:AC=4或8;
(2)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB-NB=![]() -
-![]() ==
==![]() =
=![]()
由(1)可知:此时AC=4
∴MN=![]() =2;
=2;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB+NB=![]() +
+![]() ==
==![]() =
=![]()
由(1)可知:此时AC=8
∴MN=![]() =4;
=4;
综上所述:MN=2或4;MN=![]() ;
;
(3)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC+ CN =![]() +
+![]() ==
==![]() =
=![]() =3;
=3;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC- CN =![]() -
-![]() ==
==![]() =
=![]() =3;
=3;
综上所述:MN=3;MN=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表:

(1)求a,b的值.
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,求九年级学生可捐助的贫困生中、小学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在y轴右侧且平行于y轴的直线l被反比例函数![]() (
(![]() )与函数
)与函数![]() (
(![]() )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.

【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=![]() (x>0)与函数y=
(x>0)与函数y=![]() +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.

【题型】填空题
【结束】
14
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:“2_3_5_9”,在每个“____”上,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算“____”上的符号;
,请推算“____”上的符号;
(3)在“2__3__5+9”的“__”上填入符号后,使计算所得数最小,直接写出填上符号后的算式及算式的计算结果的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题1:设a、b是方程x2+x-2012=0的两个实数根,则a2+2a+b的值为________;
问题2:方程x2-2x-1=0的两个实数根分别为x1,x2,则(x1―1)(x2―1)=_______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.

(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】良好行为习惯的养成,是中学生成长重要内容之一.某中学为了了解学生良好行为习惯养成的情况,该校七年级数学兴趣小组在校内随机抽取了部分同学进行调查评分,然后按各人得分高低分成“优秀”、“良好”、“一般”、“较差”四个等级,并绘制了如下两幅统计图(不完整):
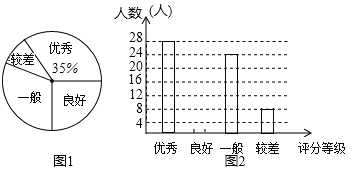
请你根据图中提供的信息,完成下列问题:
(1)图1中“优秀”部分所对应的圆心角为 .
(2)在如图2中,将“良好”部分的条形图补充完整;
(3)这次调查,良好行为习惯的养成“较差”人数占被调查人数的百分率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com