
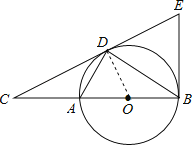
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.

【答案】解:(1)直线CD和⊙O的位置关系是相切,理由见解析
(2)BE=6.
【解析】
试题(1)连接OD,可知由直径所对的圆周角是直角可得∠DAB+∠DBA=90°,再由∠CDA=∠CBD可得∠CDA+∠ADO=90°,从而得∠CDO=90°,根据切线的判定即可得出;
(2)由已知利用勾股定理可求得DC的长,根据切线长定理有DE=EB,根据勾股定理得出方程,求出方程的解即可.
试题解析:(1)直线CD和⊙O的位置关系是相切,
理由是:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即OD⊥CE,
∴直线CD是⊙O的切线,
即直线CD和⊙O的位置关系是相切;
(2)∵AC=2,⊙O的半径是3,
∴OC=2+3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4,
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,
则(4+x)2=x2+(5+3)2,
解得:x=6,
即BE=6.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】一段长为250km的高速公路需要维修,现由甲、乙两个工程队先后接力完成,共用时15天,已知甲工程队每天维修20km,乙工程队每天维修15km.求甲、乙两个工程队分别维修了多长的高速公路?(用一元一次方程解决问题)
查看答案和解析>>
科目:初中数学 来源: 题型:
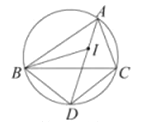
【题目】如图,I是ABC的内心,AI向延长线和△ABC的外接圆相交于点D,连接BI,BD,DC下列说法中错误的一项是( )
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI熏合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
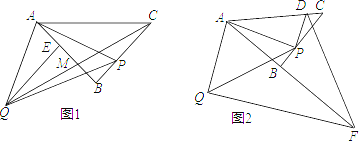
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
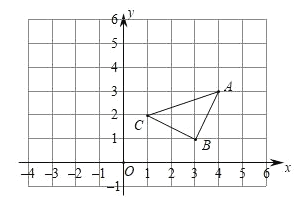
【题目】如图,若△A1B1C1是由△ABC平移后得到的,且△ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣5,y+2).
(1)在下图方格中画出△A1B1C1.
(2)求点A1、B1、C1的坐标.
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
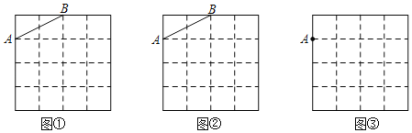
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com