
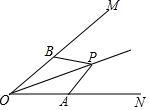
 如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可). 分析 判断两个三角形全等的方法有“SSS”,“SAS”,“ASA”,“AAS”.此题要证△AOP≌△BOP,通过题中已知的OP为∠MON的平分线,可得∠AOP=∠BOP,还有一条公共边OP=OP,若添加AO=BO,则可根据“SAS”来判定,若添加∠OAP=∠OBP,则可根据“AAS”来判定,若添加∠APO=∠BPO,则可根据“ASA”来判定.综上可得出此题的答案.
解答 解:可以添加的条件有:AO=BO,∠OAP=∠OBP,∠APO=∠BPO,
证明:∵OP为∠MON的平分线,
∴∠AOP=∠BOP,
若添加的条件为AO=BO,
在△AOP和△BOP中,
OA=OB,∠AOP=∠BOP,OP=OP,
∴△AOP≌△BOP.
所以添加的条件为AO=BO,能得到△AOP≌△BOP;
若添加的条件为∠OAP=∠OBP,
在△AOP和△BOP中,
∠OAP=∠OBP,∠AOP=∠BOP,OP=OP,
∴△AOP≌△BOP.
所以添加的条件为∠OAP=∠OBP,能得到△AOP≌△BOP;
若添加的条件为∠APO=∠BPO,
在△AOP和△BOP中,
∠AOP=∠BOP,OP=OP,∠APO=∠BPO
∴△AOP≌△BOP.
所以添加的条件为∠APO=∠BPO,能得到△AOP≌△BOP;
故答案为:AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
点评 此题属于条件开放型试题,重在考查学生全等三角形的判定,解答这类试题,需要执果索因,逆向思维,逐步探求使结论成立的条件.解决这类问题还要注意挖掘图形中的隐含条件,如公共边、对顶角相等、公共角等.这类问题的答案往往不唯一,只要合理即可.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
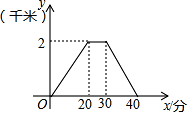 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )
某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程y(千米)与时间x(分)关系的图象,根据图象信息,下列说法正确的是( )| A. | 小王去时的速度大于回家的速度 | |
| B. | 小王去时走上坡路,回家时走下坡路 | |
| C. | 小王去时所花时间少于回家所花时间 | |
| D. | 小王在朋友家停留了10分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由-2x=3,得x=-$\frac{2}{3}$ | B. | 由-2y-3=y+1得y+2y=3+1 | ||
| C. | 由$\frac{2x-1}{3}$-1=x,得2x-1-1=3x | D. | 由$\frac{x+1}{2}$-$\frac{2x-1}{3}$=1,得3(x+1)-2(2x-1)=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com