Question

19．图1是安装在斜屋面上的热水器，图2是安装该热水器的侧面示意图．已知，斜屋面的倾斜角∠EBC=20°，长为2.1米的真空管AB与水平线BC的夹角∠ABC=37°，铁架垂直管DE的长为0.64米，求：
（1）真空管上端A到BC的距离（结果精确到0.1米）；
（2）安装热水器的铁架水平横管AD的长（结果精确到0.1米）．
（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

Answer 1

分析 （1）过A作AF⊥BC于F．构建Rt△ABF中，根据三角函数的定义与三角函数值即可求出答案；
（2）根据AB的长可求出BF的长，再判定出四边形AFDC是矩形，可求出CE与BC的长，再用BC的长减去BF的长即可解答．

解答 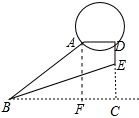解：（1）过A作AF⊥BC于F．
在Rt△ABF中，
∵sin∠ABF=$\frac{AF}{AB}$，
∴AF=ABsin∠ABF=2.1×sin37°≈1.26，
∴真空管上端A到BC的距离约为1.26米；

（2）在Rt△ABF中，
∵cos∠ABF=$\frac{BF}{AB}$，
∴BF=ABcos∠ABF=2.1×cos37°≈1.68，
∵AF⊥BC，CD⊥BC，又BC∥FD，
∴四边形AFDC是矩形，
∴AF=CD，AD=FC，
∴CE=CD-DE=1.26-0.64=0.62，
在Rt△EBC中，
∵tan∠EBC=$\frac{EC}{BC}$，
∴BC=$\frac{EC}{tan∠EBC}$=$\frac{0.62}{0.36}$=1.72，
∴AD=BC-BF=1.72-1.68=0.04（米）．
答：安装热水器的铁架水平横管AD的长为0.04米．

点评 本题考查了学生运用三角函数知识解决实际问题的能力，难度一般，熟练掌握锐角三角函数定义是解答本题的关键．